


STG等では、ある点に依存して軌跡を変えたい時があります。また画像処理ソフトのペンツールなどで点を置く毎に曲線を変化させたいこともあるでしょう。
更に、3.5、3.6章などでsin波を使った物体の移動を紹介しましたが、物体を変化させるその度合いをsin波以外の自由な曲線を使って調整したい事もあるでしょう。
そんな時、ベジェ曲線を使うと便利です。まず、ベジェ曲線には多くの次元が存在するのですが、二次方程式で表せる「二次のベジェ曲線」からご紹介します。
今、始点から出発して、終点にたどり着くまでの線が以下のようにあるとします。
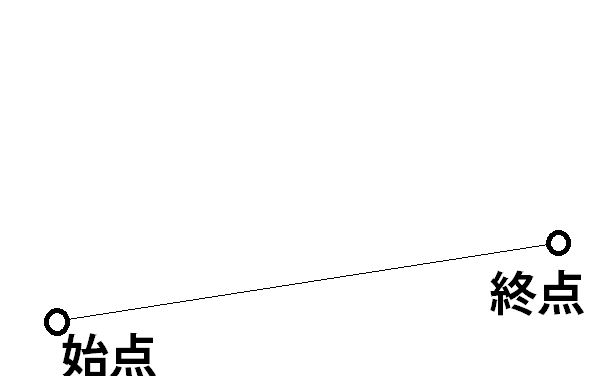
この時、「方向点」をある場所に置き、ベジェ曲線を計算すると、

このようなカーブを描きます。この曲線は以下のように
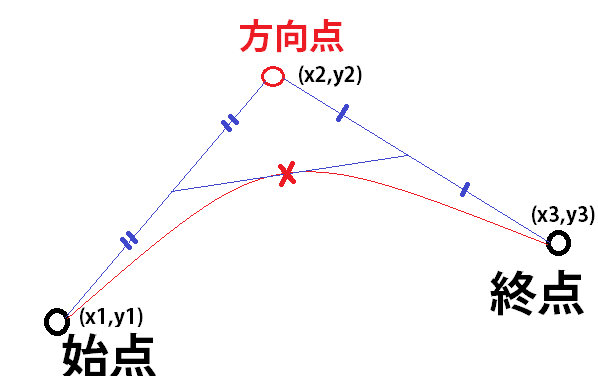
方向点とそれぞれの点を結んだ辺の長さの半分の位置を更に結んだ「×」を通る曲線です。
このように始点から終点までの間に「方向点」を置くことで、方向点に依存して変形した曲線が作れます。
この計算式はtを始点から終点まで進む時間(0~1)とすると以下のようになります。
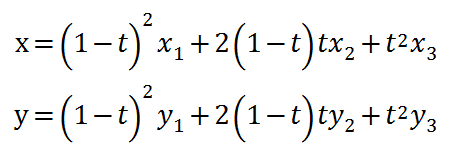
計算した(x,y)が時刻tでの位置であり、軌跡となります。
式にするとちょっと難しそうですが、なんら難しくなく、普通に足し算の2乗を展開した時のあの計算
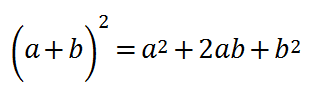
に準じて係数を付けているだけです。
ベジェ曲線の良い所は、n次方程式に対応していること。つまり何次元でもいいのです。
・・と言ってもピンと来ないと思いますが、例えば今まで二次元だった二次のベジェ曲線を一つ次元を上げて、「三次のベジェ曲線」にしてみます。
今度は、方向点を二つ持つことが出来ます。
始点である「始」から終点である「終」までの間に方向点を二つ「①」「②」の位置に置いて、ベジェ曲線を計算してみます。
このように、①にも②にも依存した動きをするようになりました。
これは座標をを以下のようにした時、

先ほどの計算式を
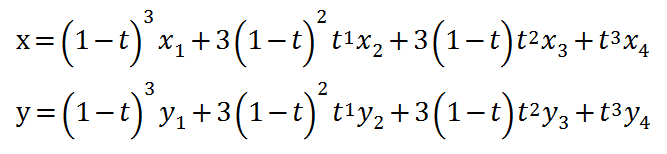
このように三次式にすることで求まります。これも見慣れぬ式の形式にすると、分かりにくいですが、なじみのある以下の式の
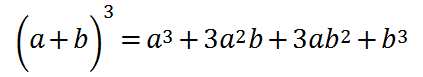
次数を係数に対応させているだけです。
(1-t)がaで、tがbであるだけですね。
では、上の動画のプログラムを実行できるサンプルを以下ご紹介します。
#include "DxLib.h" #include "Bezier.h" #define X 150 //四角形の左上座標 #define Y 20 #define W 440 //四角形の大きさ #define H 440 #define X1 0.3f //パラメータ座標1 #define Y1 0.1f #define X2 0.2f //パラメータ座標2 #define Y2 1.0f #define T 200 //時間(フレーム数) #define FSZ 40 //フォントサイズ int WINAPI WinMain(HINSTANCE,HINSTANCE,LPSTR,int){ int t=0; float x[4]={ X, X+X1*W, X+X2*W, X+W }; float y[4]={ Y, Y+Y1*H, Y+Y2*H, Y+H }; float px, py, pre_x=x[0], pre_y=y[0]; ChangeWindowMode(TRUE), DxLib_Init(), SetDrawScreen( DX_SCREEN_BACK ); SetFontSize( FSZ ); DrawBox( X, Y, X+W, Y+H, GetColor(0,255,255), FALSE ); //枠 DrawLine( X+W/2, Y, X+W/2, Y+H, GetColor(0,0,255) ); //中央線 DrawString(X+W*0 -FSZ/2, Y+H*0 -FSZ/2, "始", GetColor(255,255,255)); DrawString(X+W*X1-FSZ/2, Y+H*Y1-FSZ/2, "①", GetColor(255,255,255)); DrawString(X+W*X2-FSZ/2, Y+H*Y2-FSZ/2, "②", GetColor(255,255,255)); DrawString(X+W*1 -FSZ/2, Y+H*1 -FSZ/2, "終", GetColor(255,255,255)); while( ScreenFlip()==0 && ProcessMessage()==0 ){ if(t<T){ t ++; } else { continue; } float b = (float)t/T; float a = 1-b; px = a*a*a*x[0] + 3*a*a*b*x[1] + 3*a*b*b*x[2] + b*b*b*x[3]; py = a*a*a*y[0] + 3*a*a*b*y[1] + 3*a*b*b*y[2] + b*b*b*y[3]; DrawLine( pre_x, pre_y, px, py, GetColor(255,255,255), 6 );//軌跡描画 if( !(t%5) ){ //y成分のみ表示 DrawCircle(3,py,3,GetColor(255,0,0),TRUE); } pre_x = px;//前の位置記憶 pre_y = py; } DxLib_End(); return 0; }
定義のX1,Y1とX2,Y2が方向点です。0~1の値を色々セットして、どう変わるのか確認してみて下さい。
実際に軌跡を計算しているのは赤字部分です。
上の式をそのまま代入しているだけですね。
このようにある点に依存して終点にたどり着かせることが出来るので、STGの凝った軌跡の見せ方や、ペンツールなどに利用できるわけです。
では次の章で、もっと自由な曲線の作り方をご紹介します。
- Remical Soft -