


Sin関数を使った物体の遷移は、ヌルっと動かすことが出来ますが、サッ!っと機敏な動きを表現するのにはちょっと適しません。
つまり、sin波の曲線は、変化の度合いが滑らか過ぎて、急激な変化を表現しずらいのです。sin波というと
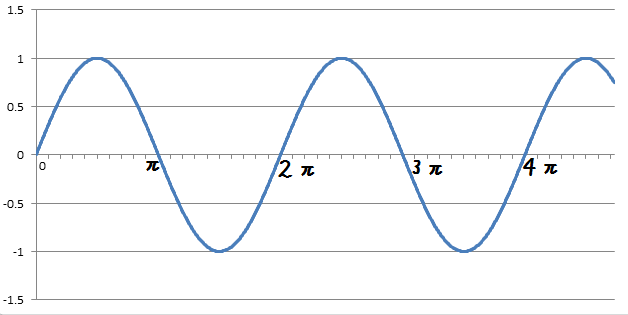
こんな曲線ですね。もっと急激に上昇して、1に近づくと、急激になだらかになるような曲線を使うともっと機敏な動きを表現することが出来そうです。
例えば軽快なUIが人気のtorneですが、機敏に感じる動き部分は恐らくsin波よりもっと急激な変化をしていることでしょう。
そこで、波のカーブを好きなように変更することを検討してみます。
まず、2次のベジェ曲線を見てみます。2次のベジェ曲線は方向点が1点だけ指定できます。この1点を左下に置いてみましょう。
すると結果以下のようになります。
(左の赤点は曲線のy成分を表現しています。曲線の動きと共にこの赤い点の動きも見て下さい。)
次に、3次のベジェ曲線は、方向点を2点置くことで、2点にひっぱられた曲線を描くことが出来ました。
この2点を重ねると更に同じ方向に引っ張ることが出来ます。方向点を2点とも画面左下に重ねた時のベジェ曲線の動きを見てみましょう。
もっと引っ張られて大袈裟にカーブする曲線が出来ました。
では更に4次のベジェ曲線にして、指定できる3点を全て左下にして、もっと左下に曲線を引っ張ってみましょう。
言いたい事は解って来たと思いますが、最後にベジェを6次にして、指定できる5点全てを左下にして、もっともっと左下に曲線を引っ張ってみましょう。
もうこれは直角なんじゃない?って位に大袈裟なカーブを描いています。
赤点の勢いを見ても、最初すごい勢いで発射し、終点に差し掛かると急に遅くなって、最後はジワジワ止まっていますね。
このようにn次元のベジェ曲線を使うとグワッと動き始めてジワッと止まる(?)ようなsin波では表現できなかった動きも可能になります。
「n次元のベジェ曲線ってどうやって計算するの?」と思うかもしれません。
(a+b)2 や (a+b)3 の展開の仕方は前章の通りで覚えている人も多いと思いますが、4次元以降は覚えていない人も多いと思います。
ここで、高校の時に習った二項定理とパスカルの三角形を思い出してください。

これです。
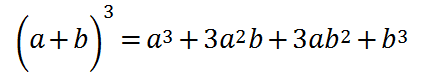
この展開式の各項の係数が1,3,3,1なのは、3次元目の段と対応付けているからですね。
ということは、4次の展開は、一つ下の段と対応させればよいことが分かり、以下のように対応付ければいいことが分かります。
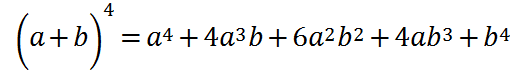
こうなればもういくつの何次元でも計算出来ますね。
この式を前章にあてはめたらいいだけなので、n次元のベジェ曲線はすぐに出来ると思います。
しかし、ベジェ曲線を使う人は、このような詳細なパラメータは見たくありません。難しい事は隠蔽すべきです。
例えば、シュッと移動するための値を取得する時にいちいち方向点座標や次元数などを教えてやらないといけないのは面倒です。
そこで、これらを簡単に扱えるベジェクラスを作ってみました。
例えば
val = Bezier.Get( 始め速く, 終わりは遅く, 現在の時刻 );
このようなパラメータの渡し方をすれば、引数時刻で指定したパラメータで動作する軌跡の位置が取得出来ます。
このパラメータですが、以下のように、遅くする5種類の度合い、等速、速くする5種類の度合い、の計11種類用意しました。
enum ePrm_t { // Prm1 / Prm2
eSlow_Lv5, // 強 ゆっくり動き始める / ゆっくり動き終える
eSlow_Lv4, // ↑ ゆっくり動き始める / ゆっくり動き終える
eSlow_Lv3, // ゆっくり動き始める / ゆっくり動き終える
eSlow_Lv2, // ↓ ゆっくり動き始める / ゆっくり動き終える
eSlow_Lv1, // 弱 ゆっくり動き始める / ゆっくり動き終える
eNoAccel, // 直線的な動きをする
eRapid_Lv1, // 弱 急に動き始める / 急に動き終える
eRapid_Lv2, // ↑ 急に動き始める / 急に動き終える
eRapid_Lv3, // 急に動き始める / 急に動き終える
eRapid_Lv4, // ↓ 急に動き始める / 急に動き終える
eRapid_Lv5, // 強 急に動き始める / 急に動き終える
};
Lvは高いほど高次式が使われるので、急激な変化になります。例えば
val = Bezier.Get( eRapid_Lv5, eSlow_lv1, 現在の時刻 );
といった渡し方をすることで、「動き初めは急激に、動き終りは弱くゆっくりで」といった指定が出来るのです。
百聞は一見に如かず。まずは見てみましょう。
以下、Bezier.hとmain.cppの2つのファイルを使いますので、新しくBezier.hを作成し、内容をコピーしてプロジェクトフォルダ内に保存して下さい。
main.cppの方は普段作業しているファイルにコピーで構いません。
Bezier.h
#ifndef DEF_BEZIER_H
#define DEF_BEZIER_H
#include <math.h>
const static int nPasTgl[12][12]={
{1},
{1,1},
{1,2,1},
{1,3,3,1},
{1,4,6,4,1},
{1,5,10,10,5,1},
{1,6,15,20,15,6,1},
{1,7,21,35,35,21,7,1},
{1,8,28,56,70,56,28,8,1},
{1,9,36,84,126,126,84,36,9,1},
{1,10,45,120,210,252,210,120,45,10,1},
{1,11,55,165,330,464,464,330,165,55,11,1}
};
class CBezier{
inline float Get( const float &y1, const float &y2, const float &t, const int &n ){
float b = t > 1 ? 1 : (t < 0 ? 0 : t);
float a = 1 - b;
float ay=0;
float y[4]={ 0, y1, y2, 1 };
int m;
for( int i=0; i<=n; i++ ){
m = i==0 ? 0 : ( i==n ? 3 : ( i <= n/2 ? 1 : 2 ));//yの添え字決定
ay += nPasTgl[n][i]*pow(a,n-i)*pow(b,i)*y[m];//※1
}
return ay;
}
public:
//Getの引数に使用するパラメータ
enum ePrm_t { // Prm1 / Prm2
eSlow_Lv5, // 強 ゆっくり動き始める / ゆっくり動き終える
eSlow_Lv4, // ↑ ゆっくり動き始める / ゆっくり動き終える
eSlow_Lv3, // ゆっくり動き始める / ゆっくり動き終える
eSlow_Lv2, // ↓ ゆっくり動き始める / ゆっくり動き終える
eSlow_Lv1, // 弱 ゆっくり動き始める / ゆっくり動き終える
eNoAccel, // 直線的な動きをする
eRapid_Lv1, // 弱 急に動き始める / 急に動き終える
eRapid_Lv2, // ↑ 急に動き始める / 急に動き終える
eRapid_Lv3, // 急に動き始める / 急に動き終える
eRapid_Lv4, // ↓ 急に動き始める / 急に動き終える
eRapid_Lv5, // 強 急に動き始める / 急に動き終える
};
/*
@brief パラメータを渡すとそれに従った曲線状の値を返す
@param[in] ePrm1 動き始めのパラメータ(ePrm_tの定義参照)
@param[in] ePrm2 動き終りのパラメータ(ePrm_tの定義参照)
@param[in] fRate 変化させたい時刻を0~1で渡す
@warning パラメータは随時変更可能
*/
float Get( ePrm_t ePrm1, ePrm_t ePrm2, float fRate ){
int n=3; //n次元指定
float y1, y2;
switch( ePrm1 ){
case eSlow_Lv5 : y1 = 0; n=11;break;//11次元
case eSlow_Lv4 : y1 = 0; n=9; break;//9次元
case eSlow_Lv3 : y1 = 0; n=7; break;//7次元
case eSlow_Lv2 : y1 = 0; n=5; break;//5次元
case eSlow_Lv1 : y1 = 0; n=3; break;//3次元
case eNoAccel : y1 = 0.333333f; n=3; break;//直線の場合は3次元中1/3の点
case eRapid_Lv1 : y1 = 1; n=3; break;//3次元
case eRapid_Lv2 : y1 = 1; n=5; break;//5次元
case eRapid_Lv3 : y1 = 1; n=7; break;//7次元
case eRapid_Lv4 : y1 = 1; n=9; break;//9次元
case eRapid_Lv5 : y1 = 1; n=11;break;//11次元
}
switch( ePrm2 ){
case eSlow_Lv5 : y2 = 1; n=11;break;//11次元
case eSlow_Lv4 : y2 = 1; n=9; break;//9次元
case eSlow_Lv3 : y2 = 1; n=7; break;//7次元
case eSlow_Lv2 : y2 = 1; n=5; break;//5次元
case eSlow_Lv1 : y2 = 1; n=3; break;//3次元
case eNoAccel : y2 = 0.6666667f; n=3; break;//直線の場合は3次元中2/3の点
case eRapid_Lv1 : y2 = 0; n=3; break;//3次元
case eRapid_Lv2 : y2 = 0; n=5; break;//5次元
case eRapid_Lv3 : y2 = 0; n=7; break;//7次元
case eRapid_Lv4 : y2 = 0; n=9; break;//9次元
case eRapid_Lv5 : y2 = 0; n=11;break;//11次元
}
return Get( y1, y2, fRate, n );
}
};
#endif
main.cpp
#include "DxLib.h" #include "Bezier.h" #define X 20 #define W 500 #define T 150 //時間(フレーム数) int WINAPI WinMain(HINSTANCE,HINSTANCE,LPSTR,int){ ChangeWindowMode(TRUE), DxLib_Init(), SetDrawScreen( DX_SCREEN_BACK ); CBezier Bez; int t=0,Img = LoadGraph("画像/キャラクタ01.png"); SetDrawMode( DX_DRAWMODE_BILINEAR ); while( ScreenFlip()==0 && ProcessMessage()==0 ){ DrawGraphF( X+Bez.Get( CBezier::eNoAccel, CBezier::eNoAccel, (float)t/T )*W, 50, Img, TRUE );//等速 DrawGraphF( X+Bez.Get( CBezier::eSlow_Lv5, CBezier::eSlow_Lv5, (float)t/T )*W, 150, Img, TRUE );//動き初め:かなりスロー、動き終り:かなりスロー DrawGraphF( X+Bez.Get( CBezier::eRapid_Lv1, CBezier::eRapid_Lv1, (float)t/T )*W, 250, Img, TRUE );//動き初め:ちょっと急、 動き終り:ちょっと急 DrawGraphF( X+Bez.Get( CBezier::eRapid_Lv5, CBezier::eSlow_Lv5, (float)t/T )*W, 350, Img, TRUE );//動き初め:かなり急、 動き終り:かなりスロー if(t<T){ t ++; } else { continue; } } DxLib_End(); // DXライブラリ終了処理 return 0; }
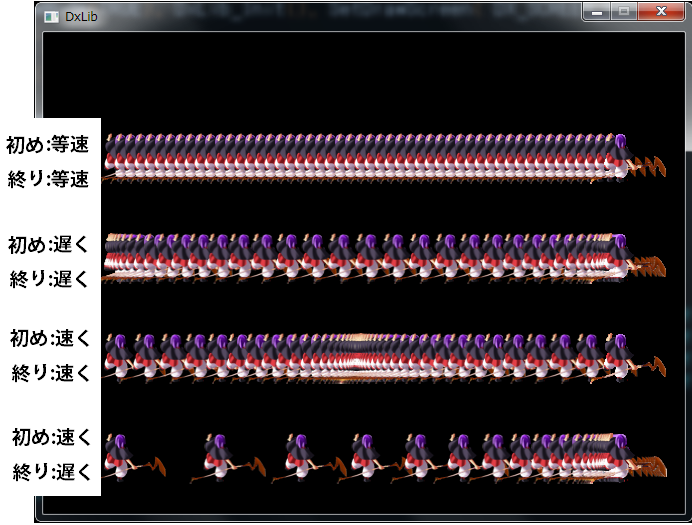
(実行結果は見やすいように少し変えています)
ベジェクラスの関数を使っているのは赤部分です。
4パターンのキャラの動きに使用しています。
例えば一番上は、初めも終わりも等速指定なので、変化なく、等速で移動しています。
上から2番目は、初めは eSlow_Lv5 を渡しているので、かなりゆっくり動き始めます。終わりは eSlow_Lv5 を渡しているのでかなりゆっくり動き終ります。
3番目は初めも終わりも速くと指定しているので、トータル時刻の辻褄を合わせるように途中で減速しています。
4番目は初めが早く、終わりがゆっくりなので、最初に言っていた「グワッと動き始めてジワッと止まる」が表現出来ています。
ベジェクラスについて、詳しい説明は省略しますが、
まずpublicなGetで引数に応じて次元と方向点の位置を決め、privateなGetで実際の計算を行っています。
※1がyの計算のみであるのは、ベジェ曲線の鉛直成分しか使用していないからです。今まで見てきた動画の左側の赤点の軌跡を使っているからですね。
そして
ay += nPasTgl[n][i]*pow(a,n-i)*pow(b,i)*y[m];
この一見意味不明な計算式ですが、高次元の方程式をバカ正直に書いているとすごく手間です。
例えば2次元のベジェ曲線なら
2a^2 + ab + b^2
だけで済みますが、11次元ともなると
a*a*a*a*a*a*a*a*a*a*a + 11*a*a*a*a*a*a*a*a*a*a*b + 55*a*a*a*a*a*a*a*a*a*b*b* + 165*a*a*a*a*a*a*a*a*b*b*b* + 330*a*a*a*a*a*.......
こんな式を延々と書かなければならなくなります。
そこで、乗算している所はn乗の計算が求まるpow関数を使い、パスカルの三角形の係数を付けて足しています。
点の座標であるy[]は最初はy[0],最後はy[3], そして前半はy[1], 後半はy[2] としています。
次元が高くなるほど方向点に重なる量が多くなり、より方向点に引っ張られた曲線になります。
sin波関数で満足できない人は一度ベジェ曲線に手を出してみてはいかがでしょうか。
- Remical Soft -