プログラマの数学について
-
たろう
プログラマの数学について
ゲームを作るために数学を勉強しようと思っているのですが、数学が苦手なのでシューティング、アクションの2Dゲームに使える数学のサイト、本などありましたら教えてください!よろしくお願いします。
-
たいちう
Re:プログラマの数学について
直接ゲーム作成に役立つわけではないですが、
特に数学が苦手ということならば、まず『プログラマの数学』という本を読んでみてはどうかと。
http://www.amazon.co.jp/dp/4797329734
特に数学が苦手ということならば、まず『プログラマの数学』という本を読んでみてはどうかと。
http://www.amazon.co.jp/dp/4797329734
-
たかぎ
Re:プログラマの数学について
高校の教科書や参考書が一番わかりやすく、内容も充実しています。
私が知る限り、高校で習う数学については(物理等への応用に必要ということも含めて)役に立たないものはひとつもありません。
もちろん、今作っているゲームでは、例えば複素数は使わないとか、そういったことはあると思います。
私が知る限り、高校で習う数学については(物理等への応用に必要ということも含めて)役に立たないものはひとつもありません。
もちろん、今作っているゲームでは、例えば複素数は使わないとか、そういったことはあると思います。
-
たいちう
Re:プログラマの数学について
持っている本だとこれかな。
『シューティングゲームアルゴリズムマニアックス』
http://www.amazon.co.jp/dp/4797327316
でも数学の解説に重点を置いているわけではありません。
この本の数学の説明が判らないがちゃんと理解したい場合、
高校の数学の教科書や参考書が一番判りやすく書かれているはずです。
『シューティングゲームアルゴリズムマニアックス』
http://www.amazon.co.jp/dp/4797327316
でも数学の解説に重点を置いているわけではありません。
この本の数学の説明が判らないがちゃんと理解したい場合、
高校の数学の教科書や参考書が一番判りやすく書かれているはずです。
-
たろう
Re:プログラマの数学について
回答ありがとうございます。
高校の数学は覚えているんので、sin()cos()などはわかるのですが。
応用が効かなくてなかなか思うようにプログラムが出来ていないのです。
応用を鍛えるにはどうすればよいのでしょうか?
高校の数学は覚えているんので、sin()cos()などはわかるのですが。
応用が効かなくてなかなか思うようにプログラムが出来ていないのです。
応用を鍛えるにはどうすればよいのでしょうか?
-
たかぎ
Re:プログラマの数学について
> 高校の数学は覚えているんので、
数学は暗記するものではないので、ちゃんと理解して身に付けましょう。
そうすれば、応用がきかないということはないと思います。
推測ですが、受験勉強しかやらなかったのではないでしょうか?
数学は暗記するものではないので、ちゃんと理解して身に付けましょう。
そうすれば、応用がきかないということはないと思います。
推測ですが、受験勉強しかやらなかったのではないでしょうか?
-
たいちう
Re:プログラマの数学について
> 応用を鍛えるにはどうすればよいのでしょうか?
まず基本を理解することです。
この場合は三角関数などの数学とサンプルプログラムですね。
どう計算したら答えが出るかとか、プログラムをどう書くかを覚えるのではなく、
どうしてこの計算で答えがでるのか、どうしてこのプログラムは
こう書いているのかを理解しましょう。
ゲームに限らずプログラミングの経験もまだ浅いことと思います。
難しい数学が関係ない分野ならば、自由にプログラムが作れるのですか?
自分の目的には遠回りに思えるかもしれませんが、基本は重要ですので、
そういう意味でも先ほど紹介した『プログラムの数学』という本はお勧めです。
まず基本を理解することです。
この場合は三角関数などの数学とサンプルプログラムですね。
どう計算したら答えが出るかとか、プログラムをどう書くかを覚えるのではなく、
どうしてこの計算で答えがでるのか、どうしてこのプログラムは
こう書いているのかを理解しましょう。
ゲームに限らずプログラミングの経験もまだ浅いことと思います。
難しい数学が関係ない分野ならば、自由にプログラムが作れるのですか?
自分の目的には遠回りに思えるかもしれませんが、基本は重要ですので、
そういう意味でも先ほど紹介した『プログラムの数学』という本はお勧めです。
-
たろう
Re:プログラマの数学について
たかぎさん回答ありがとうございます。
受験勉強は全くしませんでした(汗)理解しているつもりではいるのですが、問題を出されたらできるのですが、いざプログラムしようと思うと思い浮かびません。やっぱり応用が利かないのでしょうか。。。
たいちうさん回答ありがとうございます。
基本を理解していないと言うことでしょうか・・・サンプルプログラムを見れば理解できるのですが。
いざプログラムしろと言われたらできません。(と思います。)理解していないと言うことでしょうか・・・
「プログラムの数学」を本屋で読んでみたいと思います。
受験勉強は全くしませんでした(汗)理解しているつもりではいるのですが、問題を出されたらできるのですが、いざプログラムしようと思うと思い浮かびません。やっぱり応用が利かないのでしょうか。。。
たいちうさん回答ありがとうございます。
基本を理解していないと言うことでしょうか・・・サンプルプログラムを見れば理解できるのですが。
いざプログラムしろと言われたらできません。(と思います。)理解していないと言うことでしょうか・・・
「プログラムの数学」を本屋で読んでみたいと思います。
-
たかぎ
Re:プログラマの数学について
> 問題を出されたらできるのですが、いざプログラムしようと思うと思い浮かびません。
ということは、紙の上でなら解決できるということでしょうか?
それならプログラミングのスキルだけの問題なので、数学がどうこういうのは関係ありません。
それとも、すぐ解き始められる問題が与えられなければ、できないということでしょうか?
だとすると、それは典型的な受験勉強です。
ということは、紙の上でなら解決できるということでしょうか?
それならプログラミングのスキルだけの問題なので、数学がどうこういうのは関係ありません。
それとも、すぐ解き始められる問題が与えられなければ、できないということでしょうか?
だとすると、それは典型的な受験勉強です。
-
Dixq (管理人)
Re:プログラマの数学について
sin、cos程度であればプログラムへの応用が利かないとか難しく考える必要もないのでは^_^;
何か問題を出しましょうか。
例えば
「
0から100まで1ずつカウントアップするカウンタがあります。
これを使って、座標0,0から座標200,300へ滑らかに移動するプログラムを書きなさい
」
とかどうでしょう。
こんな事は私はいつもやるのですが、難しく考える必要もないですよね。
sin波の波形はよく活用します。
何か問題を出しましょうか。
例えば
「
0から100まで1ずつカウントアップするカウンタがあります。
これを使って、座標0,0から座標200,300へ滑らかに移動するプログラムを書きなさい
」
とかどうでしょう。
こんな事は私はいつもやるのですが、難しく考える必要もないですよね。
sin波の波形はよく活用します。
-
たかぎ
Re:プログラマの数学について
私が中学~大学のころは、紙カウンターやミニチュアフィギュア等を使ってシミュレーションゲームをやっていたので、どちらかというとこういう数学や物理は体に染み付いています。
自分でゲームを作る場合も、コンピュータは使わないので、暗算と表でいかに高速かつ正確に結果を求められるかが重要だったため、近似の取り方とかに相当苦労した記憶があります。
その意味では、コンピュータを使って計算できるのであれば楽勝なのですが、世代の違いなんでしょうね。
自分でゲームを作る場合も、コンピュータは使わないので、暗算と表でいかに高速かつ正確に結果を求められるかが重要だったため、近似の取り方とかに相当苦労した記憶があります。
その意味では、コンピュータを使って計算できるのであれば楽勝なのですが、世代の違いなんでしょうね。
-
softya
Re:プログラマの数学について
じゃあ、プログラムに関係なく純粋に数学でこれは出来ますでしょうか?
座標(50,50)の点を座標(-40,20)を中心とする回転移動で時計方向に20度回転した場合の座標は?
高校の数学が理解出来ているならすぐ出来るはずです。
座標(50,50)の点を座標(-40,20)を中心とする回転移動で時計方向に20度回転した場合の座標は?
高校の数学が理解出来ているならすぐ出来るはずです。

-
Poco
Re:プログラマの数学について
> 応用を鍛えるにはどうすればよいのでしょうか?
ゲーム作成時の問題を数学の問題に置き換えることが出来ないんですよね?
単純に問題を解く数をこなせばいいと思いますよ。
分からないことがあれば、この掲示板で聞けばいいんです。
ゲーム作成時の問題を数学の問題に置き換えることが出来ないんですよね?
単純に問題を解く数をこなせばいいと思いますよ。
分からないことがあれば、この掲示板で聞けばいいんです。
-
シエル
Re:プログラマの数学について
私も数学や物理が苦手ですので、たろうさんの気持ちはよく分かります(笑)
私が先ほど見つけた下記のサイトはいかがでしょうか?
http://hakuhin.jp/as.html
このサイトの「基本的な移動方法について」のところの記述は非常に参考になりました。
今まで画像の動作は安っぽい動きしかできなかったんですが、速度を変化させて動かせるように
なったので、少しマシな動作ができるようになりました。
C言語ではなく、FLASHのActionScriptでの解説ですが、アルゴリズムについては理解できる内容だと
思いますので、是非参考にしてみてください。
たろうさんの求めている内容と違ったらすみません。。。
私が先ほど見つけた下記のサイトはいかがでしょうか?
http://hakuhin.jp/as.html
このサイトの「基本的な移動方法について」のところの記述は非常に参考になりました。
今まで画像の動作は安っぽい動きしかできなかったんですが、速度を変化させて動かせるように
なったので、少しマシな動作ができるようになりました。
C言語ではなく、FLASHのActionScriptでの解説ですが、アルゴリズムについては理解できる内容だと
思いますので、是非参考にしてみてください。
たろうさんの求めている内容と違ったらすみません。。。
-
しろ
Re:プログラマの数学について
>> softyaさん
その問題は文系だと難しいかもしれません。今は複素平面は高校の教程の範囲外ですし、行列は基本的には文系はやらないですから。もちろん幾何と三角関数を使えば解けると思いますが・・・・・・
ちなみに私の場合、数学というより、プログラミングのスキルがまだまだなので苦労してます。
その問題は文系だと難しいかもしれません。今は複素平面は高校の教程の範囲外ですし、行列は基本的には文系はやらないですから。もちろん幾何と三角関数を使えば解けると思いますが・・・・・・
ちなみに私の場合、数学というより、プログラミングのスキルがまだまだなので苦労してます。
-
たろう
Re:プログラマの数学について
softyaさんレスありがとうざいます。(cos(-20)-40,sin(-20)+20)ですか?
すみませんわかりません。高校の数学もできない基礎自体できてなかったみたいです。
解き方教えてください。よろしくお願いします。
ぽこさんレスありがとうございます。
>単純に問題を解く数をこなせばいいと思いますよ。
>分からないことがあれば、この掲示板で聞けばいいんです。
解く数をこなせばいいのですね。ありがとうございます。
シエルさんレスありがとうございます。
このサイトありがたく参考にさせていただきます。ありがとうございます。
しろさんレスありがとうございます。
私は数学もプログラミングもなまだまだ未熟者です。
softyaさんの問題ができないくらい未熟者ですのでよろしくお願いします。
すみませんわかりません。高校の数学もできない基礎自体できてなかったみたいです。
解き方教えてください。よろしくお願いします。
ぽこさんレスありがとうございます。
>単純に問題を解く数をこなせばいいと思いますよ。
>分からないことがあれば、この掲示板で聞けばいいんです。
解く数をこなせばいいのですね。ありがとうございます。
シエルさんレスありがとうございます。
このサイトありがたく参考にさせていただきます。ありがとうございます。
しろさんレスありがとうございます。
私は数学もプログラミングもなまだまだ未熟者です。
softyaさんの問題ができないくらい未熟者ですのでよろしくお願いします。
-
たろう
Re:プログラマの数学について
もうひとつ質問させてください。
アクションゲームなどで、移動するとき、
アクションゲームなどで、移動するとき、
int a={1,1,1,1,1,1,1,1,1,1,1,1
1,1,1,0,1,0,0,0,0,1,1,1,
1,1,1,0,0,0,0,0,0,1,1,1,
1,1,1,1,1,1,1,1,1,1,1,1}
としますがこれ以外に移動させる方法ってあるのでしょうか?-
softya
Re:プログラマの数学について
>>座標(50,50)の点を座標 (-40,20)を中心とする回転移動で時計方向に20度回転した場合の座標は?
>softyaさんレスありがとうざいます。(cos(-20)-40,sin(-20)+20)ですか?
>すみませんわかりません。高校の数学もできない基礎自体できてなかったみたいです。
>解き方教えてください。よろしくお願いします。
一応行列を使って説明しますが分からなかったら聞いてください。
行列を使わなくても面倒ですが可能です。
まず分かりやすいレベルに置き換えます。
座標(50,50)をA、座標(-40,20)をBとして説明します。
(1)Bを原点に座標変換します。簡単に言うと、Bを原点に移動させる分、A-Bで座標Aを移動します。この座標をCとします。
(2)座標Cを行列で回転変換します。変換された座標はDです。
回転変換は、これです。↓
http://www.geisya.or.jp/~mwm48961/kou2/ ... mage3.html
(3)で、ずらしていた原点を元に戻します。当然座標Dも移動します。D+Bとしてやるだけです。これが座標Eです。
以上で、座標(50,50)の点を座標 (-40,20)を中心とする回転移動で時計方向に20度回転した座標であるEを求めることが出来ます。
つまり、こういう事が出来るかどうかが数学を道具として使えるかどうかって事ですね。たかぎさんの受験勉強と言っているのは、そういう事だと思います。
>softyaさんレスありがとうざいます。(cos(-20)-40,sin(-20)+20)ですか?
>すみませんわかりません。高校の数学もできない基礎自体できてなかったみたいです。
>解き方教えてください。よろしくお願いします。
一応行列を使って説明しますが分からなかったら聞いてください。
行列を使わなくても面倒ですが可能です。
まず分かりやすいレベルに置き換えます。
座標(50,50)をA、座標(-40,20)をBとして説明します。
(1)Bを原点に座標変換します。簡単に言うと、Bを原点に移動させる分、A-Bで座標Aを移動します。この座標をCとします。
(2)座標Cを行列で回転変換します。変換された座標はDです。
回転変換は、これです。↓
http://www.geisya.or.jp/~mwm48961/kou2/ ... mage3.html
(3)で、ずらしていた原点を元に戻します。当然座標Dも移動します。D+Bとしてやるだけです。これが座標Eです。
以上で、座標(50,50)の点を座標 (-40,20)を中心とする回転移動で時計方向に20度回転した座標であるEを求めることが出来ます。
つまり、こういう事が出来るかどうかが数学を道具として使えるかどうかって事ですね。たかぎさんの受験勉強と言っているのは、そういう事だと思います。
-
たろう
Re:プログラマの数学について
回答ありがとうございます。
>(3)で、ずらしていた原点を元に戻します。当然座標Dも移動します。D+Bとしてやるだけです。これが座標Eです。
はなぜ+Bなのでしょうか?
もしかして、
>(1)Bを原点に座標変換します。簡単に言うと、Bを原点に移動させる分、A-Bで座標Aを移動します。この座標をCとします。
-Bしているから、元に戻すには、+Bしてやればいいということしょうか?
>(3)で、ずらしていた原点を元に戻します。当然座標Dも移動します。D+Bとしてやるだけです。これが座標Eです。
はなぜ+Bなのでしょうか?
もしかして、
>(1)Bを原点に座標変換します。簡単に言うと、Bを原点に移動させる分、A-Bで座標Aを移動します。この座標をCとします。
-Bしているから、元に戻すには、+Bしてやればいいということしょうか?
-
たろう
Re:プログラマの数学について
>(1)Bを原点に座標変換します。簡単に言うと、Bを原点に移動させる分、A-Bで座標Aを移動します。この座標をCとします。
なぜAじゃなくBを原点にするのでしょうか?
なぜAじゃなくBを原点にするのでしょうか?
-
softya
Re:プログラマの数学について
色々聞く前にまず計算をしてみてください。
それと方眼紙に点を打って分度器で回転した座標も求めてみてください。
(1)(2)(3)をそれぞれ方眼紙でやってみるのも良いでしょう。
勉学の基本は、実際に自分でやってみることです。丸暗記じゃない数学ってそうやって理解するものですよ。
その上で分からないことは聞いてくださいね。
それと方眼紙に点を打って分度器で回転した座標も求めてみてください。
(1)(2)(3)をそれぞれ方眼紙でやってみるのも良いでしょう。
勉学の基本は、実際に自分でやってみることです。丸暗記じゃない数学ってそうやって理解するものですよ。
その上で分からないことは聞いてくださいね。
-
たろう
Re:プログラマの数学について
回答ありがとうございます。
計算してみました。
なんとか理解しました。
プログラムで実装もできました。
公式は暗記ですよね。それとも公式も理解しろと言うことでしょうか?
計算してみました。
なんとか理解しました。
プログラムで実装もできました。
公式は暗記ですよね。それとも公式も理解しろと言うことでしょうか?
-
たいちう
Re:プログラマの数学について
> 公式は暗記ですよね。それとも公式も理解しろと言うことでしょうか?
一次変換の公式ですよね?当然理解するのが望ましいです。
試験のために勉強するわけではないので暗記は必要ないですが、
覚えるとしたら公式の導き方でしょう。
他の公式でも同じです。
プログラムを作るのには結果だけが必要だ、と理解を諦めても良いですが、
その分、応用できるケースが減ります。
一次変換の公式ですよね?当然理解するのが望ましいです。
試験のために勉強するわけではないので暗記は必要ないですが、
覚えるとしたら公式の導き方でしょう。
他の公式でも同じです。
プログラムを作るのには結果だけが必要だ、と理解を諦めても良いですが、
その分、応用できるケースが減ります。
-
たかぎ
Re:プログラマの数学について
> 公式は暗記ですよね。それとも公式も理解しろと言うことでしょうか?
当然理解すべきでしょう。
小中学生なら、とりあえず公式をブラックボックスとして使うのもしかたないでしょうが、そうでなければ理解しなければ応用がききません。
プログラミングも同じで、既存の関数等の組み合わせを丸暗記するだけではまったく応用がききません。
当然理解すべきでしょう。
小中学生なら、とりあえず公式をブラックボックスとして使うのもしかたないでしょうが、そうでなければ理解しなければ応用がききません。
プログラミングも同じで、既存の関数等の組み合わせを丸暗記するだけではまったく応用がききません。
-
しろ
Re:プログラマの数学について
高校数学で理解より暗記を優先すべきものは微分積分関連の一部の公式のみです。
(厳密論をやると、大学レベルの数学まで立ち入らなければいけないので。教科書もごまかしながら説明している部分はあります。「中間値の定理」「挟み撃ちの定理」など)
ただし公式を「理解→使う」が望ましいのはわかりますが、ときにはなんとなく使ってるうちに公式を理解し、そのうち導き方も理解できる場合もあります。
最終的に理解するというのは大前提として「わからないけど、とりあえず使ってみる」というのも時には必要ですよ。
(厳密論をやると、大学レベルの数学まで立ち入らなければいけないので。教科書もごまかしながら説明している部分はあります。「中間値の定理」「挟み撃ちの定理」など)
ただし公式を「理解→使う」が望ましいのはわかりますが、ときにはなんとなく使ってるうちに公式を理解し、そのうち導き方も理解できる場合もあります。
最終的に理解するというのは大前提として「わからないけど、とりあえず使ってみる」というのも時には必要ですよ。
-
匿名
Re:プログラマの数学について
xcosθ-ysinθ,xsinθ+ycosθというのは
原点中心に図形を回転させる。(サインとコサイン)
xy座標上にある図形を原点中心に回転させるということでしょうか?
それならば次の式になりますね。
x'=xcosθ-ysinθ
y'=xsinθ+ycosθ
まず、この前にサイン、コサインがあまり分からないとのことですので
こちらをご覧ください。
http://www.urban.ne.jp/home/kz4ymnk/sem ... incos.html
直角三角形がありますね。右下に直角を位置したような直角三角形で、
ちょうどSの字を描くように(筆記体のS)
(高さ)/(斜辺)=sin(サイン)
(底辺)/(斜辺)=cos(コサイン)といいます。
このほか、タンジェントもあります。
また座標表現のところを見てみましょう。
半径rの円周上の点(x,y)の座標は、
この点と原点を結ぶ直線(半径)と、x軸とのなす角度αによって
(x,y)=(rcosα,rsinα)・・・(☆)
と表されるのです。
さて、このことを用いて、
(x,y)=(rcosα,rsinα)ですが、これをθだけ回転させた座標(x',y')とは
x軸から考えると(α+θ)だけ動かしたことになります。
ですから、(☆)において動かす角度をx軸から考えて(α+θ)だと考えると
(x',y')=(rcos(α+θ),rsin(α+θ))・・・(★)
となります。
ここで、三角関数の加法定理というのがあるのですが、
たろうさんはサイン、コサインがまだよく知らないとのことですので、
そういう定理があるんだな、とご理解ください。
それによると、
cos(α+θ)=cosαsinθ-sinαcosθ
sin(α+θ)=sinαcosθ+cosαsinθ
のようになります。
これを(★)に代入すると
x'=rcos(α+θ)=r{cosαsinθ-sinαcosθ}=rcosαsinθ-rsinαcosθ
ここでrcosα=x,rsinα=yですから
x'=xsinθ-ycosθ
同様に
y'=sin(α+θ)=r{sinαcosθ+cosαsinθ}=rsinαcosθ+rcosαcosθ
=xcosθ+ysinθ
となるので
x'=xcosθ-ysinθ
y'=xsinθ+ycosθ
がいえますね。
原点中心に図形を回転させる。(サインとコサイン)
xy座標上にある図形を原点中心に回転させるということでしょうか?
それならば次の式になりますね。
x'=xcosθ-ysinθ
y'=xsinθ+ycosθ
まず、この前にサイン、コサインがあまり分からないとのことですので
こちらをご覧ください。
http://www.urban.ne.jp/home/kz4ymnk/sem ... incos.html
直角三角形がありますね。右下に直角を位置したような直角三角形で、
ちょうどSの字を描くように(筆記体のS)
(高さ)/(斜辺)=sin(サイン)
(底辺)/(斜辺)=cos(コサイン)といいます。
このほか、タンジェントもあります。
また座標表現のところを見てみましょう。
半径rの円周上の点(x,y)の座標は、
この点と原点を結ぶ直線(半径)と、x軸とのなす角度αによって
(x,y)=(rcosα,rsinα)・・・(☆)
と表されるのです。
さて、このことを用いて、
(x,y)=(rcosα,rsinα)ですが、これをθだけ回転させた座標(x',y')とは
x軸から考えると(α+θ)だけ動かしたことになります。
ですから、(☆)において動かす角度をx軸から考えて(α+θ)だと考えると
(x',y')=(rcos(α+θ),rsin(α+θ))・・・(★)
となります。
ここで、三角関数の加法定理というのがあるのですが、
たろうさんはサイン、コサインがまだよく知らないとのことですので、
そういう定理があるんだな、とご理解ください。
それによると、
cos(α+θ)=cosαsinθ-sinαcosθ
sin(α+θ)=sinαcosθ+cosαsinθ
のようになります。
これを(★)に代入すると
x'=rcos(α+θ)=r{cosαsinθ-sinαcosθ}=rcosαsinθ-rsinαcosθ
ここでrcosα=x,rsinα=yですから
x'=xsinθ-ycosθ
同様に
y'=sin(α+θ)=r{sinαcosθ+cosαsinθ}=rsinαcosθ+rcosαcosθ
=xcosθ+ysinθ
となるので
x'=xcosθ-ysinθ
y'=xsinθ+ycosθ
がいえますね。
-
たろう
Re:プログラマの数学について
たいちうさん回答あいがとうございました。このサイト参考にさせていただいたのですが。
いまいちわかりませんでした。
匿名さんありがとうございます。
わかりやすかったです回答ありがとうございました。
ところで、定理は暗記ですよね?
いまいちわかりませんでした。
匿名さんありがとうございます。
わかりやすかったです回答ありがとうございました。
ところで、定理は暗記ですよね?
-
たかぎ
Re:プログラマの数学について
> いまいちわかりませんでした。
では、どこまでわかったのか、自分の言葉で説明してみてください。
> ところで、定理は暗記ですよね?
定理は証明を理解することが原則です。
一方、公理は暗記しかありませんが、字面を暗記するだけではなく、どういう意味かだけは理解する必要があります。
では、どこまでわかったのか、自分の言葉で説明してみてください。
> ところで、定理は暗記ですよね?
定理は証明を理解することが原則です。
一方、公理は暗記しかありませんが、字面を暗記するだけではなく、どういう意味かだけは理解する必要があります。
-
たいちう
Re:プログラマの数学について
> ところで、定理は暗記ですよね?
何かの試験を受けるつもりなのですか?
趣味でプログラムを作るだけならば、暗記の必要はありません。
本でもサイトでもノートでも好きな時に好きなだけ見てください。
応用力を付けるには理解することが大事であると、
何度も指摘されていますが、応用ができていないところを見ると、
まだ指摘を理解できていないようですね。
何かの試験を受けるつもりなのですか?
趣味でプログラムを作るだけならば、暗記の必要はありません。
本でもサイトでもノートでも好きな時に好きなだけ見てください。
応用力を付けるには理解することが大事であると、
何度も指摘されていますが、応用ができていないところを見ると、
まだ指摘を理解できていないようですね。
-
たろう
Re:プログラマの数学について
回答ありがとうございます。
>一方、公理は暗記しかありませんが、字面を暗記するだけではなく、どういう意味かだけは理解する必要があります。
意味を理解すればよいのですね。
加法定理によりx'=cos(a)cos(θ)-sin(a)sin(θ)だったら角度aをプラスθされた座標xということでいいのでしょうか。
>一方、公理は暗記しかありませんが、字面を暗記するだけではなく、どういう意味かだけは理解する必要があります。
意味を理解すればよいのですね。
加法定理によりx'=cos(a)cos(θ)-sin(a)sin(θ)だったら角度aをプラスθされた座標xということでいいのでしょうか。
-
たかぎ
Re:プログラマの数学について
> 加法定理によりx'=cos(a)cos(θ)-sin(a)sin(θ)だったら角度aをプラスθされた座標xということでいいのでしょうか。
加法定理は、その名の通り「定理」であって「公理」ではありません。
公理というのは、任意の2点を結ぶ線分は存在するとか、線分を延長して直線にすることができるとか、すべての直角は等しい角度であるといったものです。
加法定理は、その名の通り「定理」であって「公理」ではありません。
公理というのは、任意の2点を結ぶ線分は存在するとか、線分を延長して直線にすることができるとか、すべての直角は等しい角度であるといったものです。
-
たかぎ
Re:プログラマの数学について
> どういうのが公理なのでしょうか。
公理というのは、何か別のことから導かれるものではなく、「こうだ」と決めたルールのことだと考えてください。
先ほど挙げたのはユークリッド幾何学におけるの5つの公理の一部ですが、それが現実世界にも当てはまるかというと必ずしもそんなことはありません。
例えば、重力場による空間の歪がありますので、任意の2点を結ぶ線分は常に存在するわけではありません。
公理というのは、何か別のことから導かれるものではなく、「こうだ」と決めたルールのことだと考えてください。
先ほど挙げたのはユークリッド幾何学におけるの5つの公理の一部ですが、それが現実世界にも当てはまるかというと必ずしもそんなことはありません。
例えば、重力場による空間の歪がありますので、任意の2点を結ぶ線分は常に存在するわけではありません。
-
たろう
Re:プログラマの数学について
そうなんですか。
何度も質問すみません。
http://www.geisya.or.jp/~mwm48961/kou2/ ... mage3.html
のp'=xe+yfとはなぜこのような式になるのでしょうか?
何度も質問すみません。
http://www.geisya.or.jp/~mwm48961/kou2/ ... mage3.html
のp'=xe+yfとはなぜこのような式になるのでしょうか?
-
たかぎ
Re:プログラマの数学について
> http://www.geisya.or.jp/~mwm48961/kou2/ ... mage3.html
> のp'=xe+yfとはなぜこのような式になるのでしょうか?
ウェブページが開けません。
> のp'=xe+yfとはなぜこのような式になるのでしょうか?
ウェブページが開けません。
-
たろう
Re:プログラマの数学について
昨日softyaさんに紹介されたさサイトです。
http://www.geisya.or.jp/~mwm48961/kou2/ ... mage3.html
http://www.geisya.or.jp/~mwm48961/kou2/ ... mage3.html
-
Poco
Re:プログラマの数学について
応用力を鍛えるために数をこなすべし、
分からないことがあれば聞けばいい。
と言いましたが、取り組み方間違ってますよ。
少なくとも現時点で、たろうさんがどう求めていって、
どこで詰まったか、自分の考え書かなきゃ駄目ですよ。
分からないことがあれば聞けばいい。
と言いましたが、取り組み方間違ってますよ。
少なくとも現時点で、たろうさんがどう求めていって、
どこで詰まったか、自分の考え書かなきゃ駄目ですよ。
-
たろう
Re:プログラマの数学について
図で見ればわかりますが。
すみません。
なぜcos(α+θ)=cosαcosθ-sinαsinθ
sin(α+θ)=sinαcosθ+cosαsinθ
になるのか知りたいのです。理解していればできるんですよね?
すみません。
なぜcos(α+θ)=cosαcosθ-sinαsinθ
sin(α+θ)=sinαcosθ+cosαsinθ
になるのか知りたいのです。理解していればできるんですよね?
-
Poco
Re:プログラマの数学について
たろうさんに逆質問。
なんで図を見て分かったのですか?
説明願えませんか?
#私は図を見るだけではわかりませんでした。
#私は図とtoyoさんのヒントを元に自分で計算して、5分かけてようやく
#cos(α+θ)=cosαcosθ-sinαsinθ
#を導くことが出来ました。
なんで図を見て分かったのですか?
説明願えませんか?
#私は図を見るだけではわかりませんでした。
#私は図とtoyoさんのヒントを元に自分で計算して、5分かけてようやく
#cos(α+θ)=cosαcosθ-sinαsinθ
#を導くことが出来ました。
-
匿名
Re:プログラマの数学について
まずは「加法定理」について検索してみましたか?
グーグルや、ヤフーを活用してネットサーフィンすると
分かりやすく解説しているサイト様が沢山見つかると思います。
昔は教科書や書籍、先生、親を頼りに勉強するしかありませんでしたが
今は、PCを使いネットにつないで検索すれば
さまざまな分野の勉強だって調べ物だって簡単に可能な時代です。
有効活用しましょう。
http://www.google.co.jp/search?hl=ja&rl ... =&gs_rfai=
http://search.yahoo.co.jp/search?p=%E5% ... A%E7%90%86
加法定理(加法公式)といっても、
・三角関数の加法定理
・楕円関数の加法定理
・楕円曲線の加法公式
・ヤコビ多様体の加法公式
・確率の加法定理
・速度の加法定理
など、数学や物理学で使われてるさまざまなものがありますが、
たろうさんがおっしゃっているのは教育数学で使われてる"三角関数"の加法定理のことですよね?
(以下、加法定理と略)
>加法定理はどうやって求めるのでしょうか?
つまり加法定理の証明の方法が分からないと考えてよろしいですね?
加法定理の証明方法について分かりやすく解説しているお勧めのサイト様を下記に紹介しておきます。
http://w3e.kanazawa-it.ac.jp/math/categ ... iri-2.html
理解できないのであれば、先生に教えてもらいましょう。
教師は教えることのプロですから、きっと助けになってもらえるはずです。
その先生ですら分からない質問、学校で教わらない質問があれば
こちらの掲示板でまた気軽に聞いてください。
余談ですが、巨大掲示板の2chで「高校生のための数学の質問スレ」
http://find.2ch.net/?STR=%B9%E2%B9%BB%C ... LE&BBS=ALL
というスレがあります。
高校数学について困ったことがあればこちらで聞いたほうが確実に正確な答えが返ってくると思います。
ただし、こんなに丁寧に回答してくれる方はいませんけど。
一応、ここは"C言語の"なんでも質問掲示板なので、本格的な数学についての質問はそちらで聞くと良いでしょう。
話は戻りますが、加法定理の証明を見ると分かると思いますが、
いちいちこれらの計算をして加法定理を求めてから活用するのは面倒ですよね?
なのでこれは暗記するのが一般的です。大幅な時間短縮になります。
有名な暗記方法で
咲いたコスモス コスモス咲いた
sinα cosβ + cosα sinβ
等あります。
加法定理の覚え方は下記のサイト様が
面白い覚え方も含め、沢山書かれてあります。
自分が一番覚えやすいと思う方法で暗記するとよいでしょう。
http://www.d2.dion.ne.jp/~hmurata/goro/kahou.html
たろうさんは中学生か高校生の方でしょうか?
私の時代は中学時代に加法定理を学びましたが、現代の教育では高校2年生の時に学びます。
まだ習ってないこと、分からないことについて自ら学ぼうとする意欲は大変素晴らしいですね。
これからも頑張ってください。
グーグルや、ヤフーを活用してネットサーフィンすると
分かりやすく解説しているサイト様が沢山見つかると思います。
昔は教科書や書籍、先生、親を頼りに勉強するしかありませんでしたが
今は、PCを使いネットにつないで検索すれば
さまざまな分野の勉強だって調べ物だって簡単に可能な時代です。
有効活用しましょう。
http://www.google.co.jp/search?hl=ja&rl ... =&gs_rfai=
http://search.yahoo.co.jp/search?p=%E5% ... A%E7%90%86
加法定理(加法公式)といっても、
・三角関数の加法定理
・楕円関数の加法定理
・楕円曲線の加法公式
・ヤコビ多様体の加法公式
・確率の加法定理
・速度の加法定理
など、数学や物理学で使われてるさまざまなものがありますが、
たろうさんがおっしゃっているのは教育数学で使われてる"三角関数"の加法定理のことですよね?
(以下、加法定理と略)
>加法定理はどうやって求めるのでしょうか?
つまり加法定理の証明の方法が分からないと考えてよろしいですね?
加法定理の証明方法について分かりやすく解説しているお勧めのサイト様を下記に紹介しておきます。
http://w3e.kanazawa-it.ac.jp/math/categ ... iri-2.html
理解できないのであれば、先生に教えてもらいましょう。
教師は教えることのプロですから、きっと助けになってもらえるはずです。
その先生ですら分からない質問、学校で教わらない質問があれば
こちらの掲示板でまた気軽に聞いてください。
余談ですが、巨大掲示板の2chで「高校生のための数学の質問スレ」
http://find.2ch.net/?STR=%B9%E2%B9%BB%C ... LE&BBS=ALL
というスレがあります。
高校数学について困ったことがあればこちらで聞いたほうが確実に正確な答えが返ってくると思います。
ただし、こんなに丁寧に回答してくれる方はいませんけど。
一応、ここは"C言語の"なんでも質問掲示板なので、本格的な数学についての質問はそちらで聞くと良いでしょう。
話は戻りますが、加法定理の証明を見ると分かると思いますが、
いちいちこれらの計算をして加法定理を求めてから活用するのは面倒ですよね?
なのでこれは暗記するのが一般的です。大幅な時間短縮になります。
有名な暗記方法で
咲いたコスモス コスモス咲いた
sinα cosβ + cosα sinβ
等あります。
加法定理の覚え方は下記のサイト様が
面白い覚え方も含め、沢山書かれてあります。
自分が一番覚えやすいと思う方法で暗記するとよいでしょう。
http://www.d2.dion.ne.jp/~hmurata/goro/kahou.html
たろうさんは中学生か高校生の方でしょうか?
私の時代は中学時代に加法定理を学びましたが、現代の教育では高校2年生の時に学びます。
まだ習ってないこと、分からないことについて自ら学ぼうとする意欲は大変素晴らしいですね。
これからも頑張ってください。
-
たろう
Re:プログラマの数学について
わかるといったのは単純に見て思っただけです。なぜこうなったか図だけではわかっていないです。
どうやってできたのでしょうか?図とtoyoさんのヒントだけでどうやってできたのでしょうか?
教えてください。
どうやってできたのでしょうか?図とtoyoさんのヒントだけでどうやってできたのでしょうか?
教えてください。
-
Poco
Re:プログラマの数学について
> わかるといったのは単純に見て思っただけです。なぜこうなったか図だけではわかっていないです。
> どうやってできたのでしょうか?図とtoyoさんのヒントだけでどうやってできたのでしょうか?
> 教えてください。
toyoさんは、図を示された上で
A-B = A'-B'を求めろと言っています。
ここにはsin,cosがありません。
つまり、A-BやA'-B'をsin,cosで表わして等式で結ぶと何かが出てくることを示唆しています。
それを行っただけです。
追記:
ちなみに、最初私はtoyoさんが提示された導出法とは別のやり方で
加法定理を導出しました。
> どうやってできたのでしょうか?図とtoyoさんのヒントだけでどうやってできたのでしょうか?
> 教えてください。
toyoさんは、図を示された上で
A-B = A'-B'を求めろと言っています。
ここにはsin,cosがありません。
つまり、A-BやA'-B'をsin,cosで表わして等式で結ぶと何かが出てくることを示唆しています。
それを行っただけです。
追記:
ちなみに、最初私はtoyoさんが提示された導出法とは別のやり方で
加法定理を導出しました。

-
たろう
Re:プログラマの数学について
匿名さん回答ありがとうございます。
高校2年です。加法定理はまだ習ってないです。
先生に聞いてみます。
サイトも参考にさせていただきます。
ありがとうございます!
暗記といっても実際説明できないと話にならないですよね?
高校2年です。加法定理はまだ習ってないです。
先生に聞いてみます。
サイトも参考にさせていただきます。
ありがとうございます!
暗記といっても実際説明できないと話にならないですよね?
-
しろ
Re:プログラマの数学について
加法定理の証明はまぁ一度自分で導出できれば、それでいいかと。あとは覚えて使えるようになりましょう。
toyoさんの図を用いた証明は有名ですが、0から自分で思いついて証明できるものではなかなかないと思います。
(図があれば、導くことは容易ですが)
ほかにも複素平面を用いた証明などがよく知られています。
なお、98年の東大前期で加法定理の証明が出題されています。
正答率はあまりよくなかったらしいですよ。
toyoさんの図を用いた証明は有名ですが、0から自分で思いついて証明できるものではなかなかないと思います。
(図があれば、導くことは容易ですが)
ほかにも複素平面を用いた証明などがよく知られています。
なお、98年の東大前期で加法定理の証明が出題されています。
正答率はあまりよくなかったらしいですよ。
-
しろ
Re:プログラマの数学について
>>加法定理を導く上で一番簡単なのは、回転行列を2つ掛ける方法ですね
確かにそれもありましたね。本質的には複素平面と同じでしょうか。
まぁそろそろ話題がずれてきたのでこのへんで辞めておきます。
確かにそれもありましたね。本質的には複素平面と同じでしょうか。
まぁそろそろ話題がずれてきたのでこのへんで辞めておきます。
-
匿名
Re:プログラマの数学について
>暗記といっても実際説明できないと話にならないですよね?
加法定理の場合、
世の中、加法定理を説明する機会より、
加法定理を応用する機会のほうが多いと思います。
一番最初の質問に戻りますが、
>ゲームを作るために数学を勉強しようと思っている
のならば、プログラムで加法定理を証明するわけではない限り、
加法定理を使ってゲームを作る機会のほうが多いのではないでしょうか。
そういう意味では、説明することは大事ですが、
活用する力(応用力)をつけることのほうがもっと大事だと思います。
しろさんがおっしゃるとおり、加法定理の証明を理解するのはなかなか難しいです。
当時教えていた数学教師は加法定理の証明は「理解しなくてもいい」と言うほどでしたので。
大切なのは加法定理自体とその応用です。でも加法定理の証明を理解しても損はありません。
ただ、理解する時間があるのならば、他の勉強にその時間を当てることをおススメします。
教師を目指していたり、大学で数学科、物理学科に入る等の目的ならば話は別ですけど。
まあ、自分の子供が出来た時に
子供が「加法定理って何?」と聞かれたときにスラスラ言えるとかっこいいですけどねw
加法定理の場合、
世の中、加法定理を説明する機会より、
加法定理を応用する機会のほうが多いと思います。
一番最初の質問に戻りますが、
>ゲームを作るために数学を勉強しようと思っている
のならば、プログラムで加法定理を証明するわけではない限り、
加法定理を使ってゲームを作る機会のほうが多いのではないでしょうか。
そういう意味では、説明することは大事ですが、
活用する力(応用力)をつけることのほうがもっと大事だと思います。
しろさんがおっしゃるとおり、加法定理の証明を理解するのはなかなか難しいです。
当時教えていた数学教師は加法定理の証明は「理解しなくてもいい」と言うほどでしたので。
大切なのは加法定理自体とその応用です。でも加法定理の証明を理解しても損はありません。
ただ、理解する時間があるのならば、他の勉強にその時間を当てることをおススメします。
教師を目指していたり、大学で数学科、物理学科に入る等の目的ならば話は別ですけど。
まあ、自分の子供が出来た時に
子供が「加法定理って何?」と聞かれたときにスラスラ言えるとかっこいいですけどねw

-
たかぎ
Re:プログラマの数学について
> 子供が「加法定理」って何?って聞かれたときにスラスラ言えるとかっこいいですけどねw
証明できるかどうかはともかく、加法定理が何かぐらい子供に説明できないと恥ずかしいですよ。
第一、何かわからない定理は使うことすらできません。
例えば、「清宮の定理」という言葉を聞いて、それが何か分からなければ何の応用価値もありませんよね。それといっしょです。
加法定理に限らず、どんな定理でもそうですが、それを証明する機会より利用する機会が多いことは間違いありません。
けれども、定理を証明できるのであれば、証明の過程で得た知見をいかすことで、類似の命題に対して応用がききます。
これが大事なのです。
プログラミングでも同じことで、汎用の関数やクラス(例えば標準ライブラリに含まれるようなもの)というのは、実装するより利用する機会のほうが圧倒的に多いのですが、実際に内部を理解しておく(できれば自分で実装してみる)と、応用力が格段に高まることは間違いありません。
こうしたプリミティブな内容の理解や実装経験を積まなければ、結局は既存のもののパッチワークしかできなくなってしまいます。
もちろん、目先の問題としてそれでもよいでしょう。一度にすべてを理解することは困難ですし、現実的でもありません。
けれども、理解する努力をするのと、理解を放棄して有り物を組み合わせるだけに徹するのでは、将来的にその人の実力の限界に大きな差を生じます。
証明できるかどうかはともかく、加法定理が何かぐらい子供に説明できないと恥ずかしいですよ。
第一、何かわからない定理は使うことすらできません。
例えば、「清宮の定理」という言葉を聞いて、それが何か分からなければ何の応用価値もありませんよね。それといっしょです。
加法定理に限らず、どんな定理でもそうですが、それを証明する機会より利用する機会が多いことは間違いありません。
けれども、定理を証明できるのであれば、証明の過程で得た知見をいかすことで、類似の命題に対して応用がききます。
これが大事なのです。
プログラミングでも同じことで、汎用の関数やクラス(例えば標準ライブラリに含まれるようなもの)というのは、実装するより利用する機会のほうが圧倒的に多いのですが、実際に内部を理解しておく(できれば自分で実装してみる)と、応用力が格段に高まることは間違いありません。
こうしたプリミティブな内容の理解や実装経験を積まなければ、結局は既存のもののパッチワークしかできなくなってしまいます。
もちろん、目先の問題としてそれでもよいでしょう。一度にすべてを理解することは困難ですし、現実的でもありません。
けれども、理解する努力をするのと、理解を放棄して有り物を組み合わせるだけに徹するのでは、将来的にその人の実力の限界に大きな差を生じます。
-
たいちう
Re:プログラマの数学について
> 加法定理の方の応用を勉強したいと思います。プログラムのほうに力をいれていきたいと思います。
匿名さんの考えとは違うのですが、理解できないと応用はできないのです。
加法定理をブラックボックスとみなして、使い方だけ何通りか覚えることは可能ですが、
覚えた使い方以外の事、すなわち、応用は期待できないでしょう。
また、今高校2年生との事ですが、加法定理程度のものを理解不能なブラックボックスとしてしまうと、
たろうさんの数学の世界はたいそう暗いものになってしまいますよ。
匿名さんの考えとは違うのですが、理解できないと応用はできないのです。
加法定理をブラックボックスとみなして、使い方だけ何通りか覚えることは可能ですが、
覚えた使い方以外の事、すなわち、応用は期待できないでしょう。
また、今高校2年生との事ですが、加法定理程度のものを理解不能なブラックボックスとしてしまうと、
たろうさんの数学の世界はたいそう暗いものになってしまいますよ。
-
Dixq (管理人)
Re:プログラマの数学について
ブラックボックス化してしまうと、勉強も楽しくなくなっちゃうんですよね。
意味も解らず計算に使うと、計算結果も「コレ何が出たの?」って状態になって魅力を感じなくなると思います。
プログラムにおいては、計算結果が出ればいいって場合があるでしょうから、魅力はそこに感じなくてもいい場合もあるかもしれませんが、
数学をエンジョイするなら、やはり何故?何故?と意欲的に理解を深める必要があるでしょう。
私の経験で言うと、初めて行列計算を習った時、
何の為にこんな変な掛け算の仕方をしなければならないのか、全く理解できず、
先生に聞いても特に何に使うのか教えてくれず、
何の魅力も感じませんでした。
しかし大学で線形代数を学んでからやっとその意味が解り、面白くなりました。
そのうちブラックボックス化しないとやってられない分野にも遭遇するでしょうから若いうちはなるべくブラックボックスにしない事が望ましいですねぇ・・。
意味も解らず計算に使うと、計算結果も「コレ何が出たの?」って状態になって魅力を感じなくなると思います。
プログラムにおいては、計算結果が出ればいいって場合があるでしょうから、魅力はそこに感じなくてもいい場合もあるかもしれませんが、
数学をエンジョイするなら、やはり何故?何故?と意欲的に理解を深める必要があるでしょう。
私の経験で言うと、初めて行列計算を習った時、
何の為にこんな変な掛け算の仕方をしなければならないのか、全く理解できず、
先生に聞いても特に何に使うのか教えてくれず、
何の魅力も感じませんでした。
しかし大学で線形代数を学んでからやっとその意味が解り、面白くなりました。
そのうちブラックボックス化しないとやってられない分野にも遭遇するでしょうから若いうちはなるべくブラックボックスにしない事が望ましいですねぇ・・。
-
たかぎ
Re:プログラマの数学について
> 先生に聞いても特に何に使うのか教えてくれず、
> 何の魅力も感じませんでした。
これはありますね。
私は学校で教えるときには、ざっと概要を説明した後、「これが使えると、どんなおいしいことがあるのか」ということを話すようにしています。
三角関数や行列のような数学もそうですし、ポインタとか再帰呼び出しなどのプログラミング的なこともそうです。
> 何の魅力も感じませんでした。
これはありますね。
私は学校で教えるときには、ざっと概要を説明した後、「これが使えると、どんなおいしいことがあるのか」ということを話すようにしています。
三角関数や行列のような数学もそうですし、ポインタとか再帰呼び出しなどのプログラミング的なこともそうです。
-
匿名
Re:プログラマの数学について
>私の経験で言うと、初めて行列計算を習った時、
>何の為にこんな変な掛け算の仕方をしなければならないのか、全く理解できず、
>先生に聞いても特に何に使うのか教えてくれず、
>何の魅力も感じませんでした。
その理由は教科書のまえがきに書いてあるから
あえてその先生は自分で調べさせるために何も教えなかったんじゃないかな。
良い先生ですね。
>何の為にこんな変な掛け算の仕方をしなければならないのか、全く理解できず、
>先生に聞いても特に何に使うのか教えてくれず、
>何の魅力も感じませんでした。
その理由は教科書のまえがきに書いてあるから
あえてその先生は自分で調べさせるために何も教えなかったんじゃないかな。
良い先生ですね。
-
Dixq (管理人)
Re:プログラマの数学について
そうでしょうか。数Cの教科書が手元に無いのでわかりませんが、
数学の導入ページに書いてあることなんて、せいぜいwikiに書いてある事位じゃないでしょうか。
それが具体的に何に応用出来て、どういう魅力があるのかなんて、解るように書いてあったかな・・。
wiki引用[color=Tea[/url]
数学において、行列(ぎょうれつ、matrix)とは、ある固定された環の元を矩形(長方形)状に並べたものである。特に、すべての成分が実数の行列を実行列、すべての成分が複素数の行列を複素行列という。
同じサイズの行列の集合はアーベル群の構造を持ち、更に同じサイズの正方行列全体はひとつの環をなすので、行列の集合それ自体が代数学の対象である。また、行列は線形写像の表示手段として数学の様々な場面で現れ、数学を道具とする自然科学や工学の各分野でも基本的な道具としての位置を占める。
行列の起源は連立一次方程式の解法にある。例えば、加減法とも呼ばれる方程式の解法を定式化したものとして行列の基本変形や、それによるガウスの消去法などのアルゴリズムが挙げられる。これは三角化・対角化や逆行列の計算などに広範に適用できる。[/color]
まぁもっと砕いてあるかも知れませんが、似たような説明を高校生が見て魅力を持つとは思えません・・。
仮に何か書いてあったとしても、それを教えてくれない先生は良い先生とは思わないです。
少なくとも自分で調べる力を付けさせたいとは思っていない、
思っていたら
「調べてみよう、調べて解らなかったら聞きにおいで」とか
「教科書のどこかにそれが書いてあるからみてごらん」とか何か言ってくれると思います。
先生ならその分野に興味を持たせるような何らかのサポートをしてほしいものです。
数学を好きにしようとしてくれる先生は実際少ないですよねぇ。
数学の導入ページに書いてあることなんて、せいぜいwikiに書いてある事位じゃないでしょうか。
それが具体的に何に応用出来て、どういう魅力があるのかなんて、解るように書いてあったかな・・。
wiki引用[color=Tea[/url]
数学において、行列(ぎょうれつ、matrix)とは、ある固定された環の元を矩形(長方形)状に並べたものである。特に、すべての成分が実数の行列を実行列、すべての成分が複素数の行列を複素行列という。
同じサイズの行列の集合はアーベル群の構造を持ち、更に同じサイズの正方行列全体はひとつの環をなすので、行列の集合それ自体が代数学の対象である。また、行列は線形写像の表示手段として数学の様々な場面で現れ、数学を道具とする自然科学や工学の各分野でも基本的な道具としての位置を占める。
行列の起源は連立一次方程式の解法にある。例えば、加減法とも呼ばれる方程式の解法を定式化したものとして行列の基本変形や、それによるガウスの消去法などのアルゴリズムが挙げられる。これは三角化・対角化や逆行列の計算などに広範に適用できる。[/color]
まぁもっと砕いてあるかも知れませんが、似たような説明を高校生が見て魅力を持つとは思えません・・。
仮に何か書いてあったとしても、それを教えてくれない先生は良い先生とは思わないです。
少なくとも自分で調べる力を付けさせたいとは思っていない、
思っていたら
「調べてみよう、調べて解らなかったら聞きにおいで」とか
「教科書のどこかにそれが書いてあるからみてごらん」とか何か言ってくれると思います。
先生ならその分野に興味を持たせるような何らかのサポートをしてほしいものです。
数学を好きにしようとしてくれる先生は実際少ないですよねぇ。
-
たろう
Re:プログラマの数学について
たかぎさん回答ありがとうございます。
>証明できるかどうかはともかく、加法定理が何かぐらい子供に説明できないと恥ずかしいですよ。
加法定理とは角度と角度を足したときに求まる(x,y)というものとこんな感じにいえばよいのでしょうか?
たいちうさん回答ありがとうございます。
加法定理とは角度と角度を足したときに求まる(x,y)というものとこんな感じにいえばよいのでしょうか?
Dixq (管理人)さん
回答ありがとうございます。
なんとかして理解しようと思います。
加法定理とは角度と角度を足したときに求まる(x,y)というものとこんな感じにいえばよいのでしょうか?
という答えではダメでしょうか?
>証明できるかどうかはともかく、加法定理が何かぐらい子供に説明できないと恥ずかしいですよ。
加法定理とは角度と角度を足したときに求まる(x,y)というものとこんな感じにいえばよいのでしょうか?
たいちうさん回答ありがとうございます。
加法定理とは角度と角度を足したときに求まる(x,y)というものとこんな感じにいえばよいのでしょうか?
Dixq (管理人)さん
回答ありがとうございます。
なんとかして理解しようと思います。
加法定理とは角度と角度を足したときに求まる(x,y)というものとこんな感じにいえばよいのでしょうか?
という答えではダメでしょうか?
-
たかぎ
Re:プログラマの数学について
> 加法定理とは角度と角度を足したときに求まる(x,y)というものとこんな感じにいえばよいのでしょうか?
本当に理解できていますか?
せめて、「2つの角度の和に対する正弦・余弦・正接を、もとの角度の正弦・余弦・正接を用いて表すやりかた」ぐらいのことをいってください。

本当に理解できていますか?
せめて、「2つの角度の和に対する正弦・余弦・正接を、もとの角度の正弦・余弦・正接を用いて表すやりかた」ぐらいのことをいってください。

-
たかぎ
Re:プログラマの数学について
> 数Cの教科書
学校の教科書は出版社によってかなり異なります。
数学の教科書は、歴史なんかに比べればずっとましですが、それでも「まえがき」なんか、余計なことさえ書かなければ何を書いてもよいので、一般論として取り上げられるようなものではありません。
学校の教科書は出版社によってかなり異なります。
数学の教科書は、歴史なんかに比べればずっとましですが、それでも「まえがき」なんか、余計なことさえ書かなければ何を書いてもよいので、一般論として取り上げられるようなものではありません。
-
たろう
Re:プログラマの数学について
せめて、「2つの角度の和に対するsin(a)・cos(a)を、もとの角度のsin(a')・cos(a')を用いて表すやりかた」ぐらいのことをいってください。
ということでしょうか?
ということでしょうか?
-
たいちう
Re:プログラマの数学について
どう言ったらよいでしょうか?ではないのです。
理解度に応じた表現が出来るはずですので理解度を高めて下さい。
表現力のみを磨こうというのは間違ってます。
理解度に応じた表現が出来るはずですので理解度を高めて下さい。
表現力のみを磨こうというのは間違ってます。
-
Dixq (管理人)
Re:プログラマの数学について
コメント一つ内にマルチポスト状態・・^^;
えぇと、
「角度と角度を足したときに求まる(x,y)」という表現が微妙なので・・
ちょっと図を作ってみました。
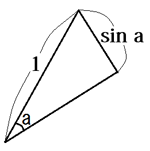
角度aに対して、図の部分、sin aになりますよね。
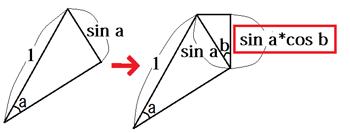
赤四角の部分は更にcos bしたものですよね?
ということで、ここは、sin a*cos bになります。
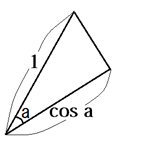
一方で、角度aに対して図の部分、cos aになりますよね。
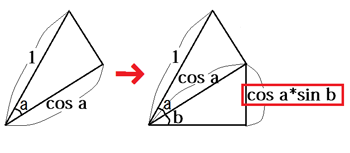
赤四角の部分は更にsin bしたものですよね?
ということで、ここは、cos a*sin bになります。
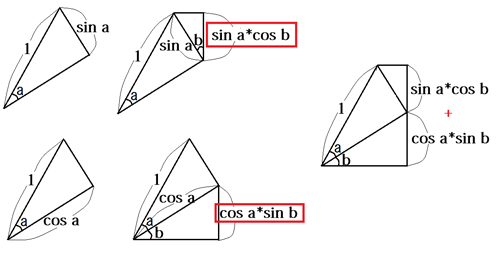
2つ足し合わせると、a+bのsinが求まるという事です。なので、
sin(a+b) = sin a*cos b + cos a*sin b
となるという事です。
えぇと、
「角度と角度を足したときに求まる(x,y)」という表現が微妙なので・・
ちょっと図を作ってみました。

角度aに対して、図の部分、sin aになりますよね。

赤四角の部分は更にcos bしたものですよね?
ということで、ここは、sin a*cos bになります。

一方で、角度aに対して図の部分、cos aになりますよね。

赤四角の部分は更にsin bしたものですよね?
ということで、ここは、cos a*sin bになります。

2つ足し合わせると、a+bのsinが求まるという事です。なので、
sin(a+b) = sin a*cos b + cos a*sin b
となるという事です。
-
a
Re:プログラマの数学について
>たかぎさん
日本の公立の高校数学では数研出版が一般的でしょう。
むしろ数研出版を知らない子供がいたら珍しいですね。
「余計なことさえ書かなければ何を書いてもよい」
という根拠のソースが全くないので事実かどうかは不明ですが、
あくまでも高等学校向けの文部科学省検定済教科書なのにそれだと問題でしょう。
全国の子供が使う教科書でまえがきが適当に書かれてて
それを真にうけとめる子供がいたとしたら(ry
日本の公立の高校数学では数研出版が一般的でしょう。
むしろ数研出版を知らない子供がいたら珍しいですね。
「余計なことさえ書かなければ何を書いてもよい」
という根拠のソースが全くないので事実かどうかは不明ですが、
あくまでも高等学校向けの文部科学省検定済教科書なのにそれだと問題でしょう。
全国の子供が使う教科書でまえがきが適当に書かれてて
それを真にうけとめる子供がいたとしたら(ry
-
たかぎ
Re:プログラマの数学について
> 日本の公立の高校数学では数研出版が一般的でしょう。
> むしろ数研出版を知らない子供がいたら珍しいですね。
数研が多いのは確かでしょうね。
# 私のときもそうでしたし。
ただ、他の教科書がないわけではありませんので、数研を使っているのが当たり前のような主張は正しくないでしょう。
> 「余計なことさえ書かなければ何を書いてもよい」
> という根拠のソースが全くないので事実かどうかは不明ですが、
> あくまでも高等学校向けの文部科学省検定済教科書なのにそれだと問題でしょう。
http://www.mext.go.jp/a_menu/shotou/kyo ... 990402.htmによると、
[color=#faa>
[数学科]
1 範囲及び程度
(1) 「数学B」及び「数学C」においては,学習指導要領に示す項目のすべてを取り上げていること。
(2) 「数学C」においては,必要な限りにおいて数学科の他の科目の内容を関連付けて扱っても差し支えないこと。
2 選択・扱い及び組織・分量
(1) 定理,公式等の知識や計算技能の習得に偏ることなく,各学習内容について,そのねらい,有用性及び前後の学習内容との関連が明らかになるよう配慮されていること。
[/color]
ですので、必要なことが盛り込まれてさえいれば、まえがきには「一所懸命書いたので、しっかり勉強してください」といった趣旨のことしか書いていなくても基準は満たします。
http://www.mext.go.jp/b_menu/shuppan/so ... 03/005.htmにある目標を盛り込むのが正攻法だとは思いますが、それをまえがきに書かないといけないとは決まっていませんね。
> 全国の子供が使う教科書でまえがきが適当に書かれてて
> それを真にうけとめる子供がいたとしたら(ry
だから余計なことは書いたらダメなんです。
先ほどの検定基準にも、
[color=gray>
第2章 各教科共通の条件
1 範囲及び程度
(1) 高等学校学習指導要領(平成11年文部省告示第58号。以下「学習指導要領」という。)に示す教科及び科目の「目標」(以下「学習指導要領に示す目標」という。)に従い,学習指導要領に示す科目の「内容」(以下「学習指導要領に示す内容」という。)及び「内容の取扱い」(「各科目にわたる 指導計画の作成と内容の取扱い」及び「各科目にわたる内容 の取扱い」を含む。以下「学習指導要領に示す内容の取扱い」 という。)に示す事項を不足なく取り上げていること。[/color]
[color=#faa>(2) 本文,問題,説明文,注,資料,作品,挿絵,写真,図など教科用図書の内容(以下「図書の内容」という。)には,学習指導要領に示す目標,学習指導要領に示す内容及び学習指導要領に示す内容の取扱いに照らして,不必要なものは取り上げていないこと。[/color]
[color=gray>(3) 図書の内容は,生徒の心身の発達段階に適応しており,その能力からみて程度が高過ぎるところはないこと。
[/color]
とありますから。
もっとも、歴史教科書とかには、余計なことが書かれているケースが多々あるわけですが...

> むしろ数研出版を知らない子供がいたら珍しいですね。
数研が多いのは確かでしょうね。
# 私のときもそうでしたし。
ただ、他の教科書がないわけではありませんので、数研を使っているのが当たり前のような主張は正しくないでしょう。
> 「余計なことさえ書かなければ何を書いてもよい」
> という根拠のソースが全くないので事実かどうかは不明ですが、
> あくまでも高等学校向けの文部科学省検定済教科書なのにそれだと問題でしょう。
http://www.mext.go.jp/a_menu/shotou/kyo ... 990402.htmによると、
[color=#faa>
[数学科]
1 範囲及び程度
(1) 「数学B」及び「数学C」においては,学習指導要領に示す項目のすべてを取り上げていること。
(2) 「数学C」においては,必要な限りにおいて数学科の他の科目の内容を関連付けて扱っても差し支えないこと。
2 選択・扱い及び組織・分量
(1) 定理,公式等の知識や計算技能の習得に偏ることなく,各学習内容について,そのねらい,有用性及び前後の学習内容との関連が明らかになるよう配慮されていること。
[/color]
ですので、必要なことが盛り込まれてさえいれば、まえがきには「一所懸命書いたので、しっかり勉強してください」といった趣旨のことしか書いていなくても基準は満たします。
http://www.mext.go.jp/b_menu/shuppan/so ... 03/005.htmにある目標を盛り込むのが正攻法だとは思いますが、それをまえがきに書かないといけないとは決まっていませんね。
> 全国の子供が使う教科書でまえがきが適当に書かれてて
> それを真にうけとめる子供がいたとしたら(ry
だから余計なことは書いたらダメなんです。
先ほどの検定基準にも、
[color=gray>
第2章 各教科共通の条件
1 範囲及び程度
(1) 高等学校学習指導要領(平成11年文部省告示第58号。以下「学習指導要領」という。)に示す教科及び科目の「目標」(以下「学習指導要領に示す目標」という。)に従い,学習指導要領に示す科目の「内容」(以下「学習指導要領に示す内容」という。)及び「内容の取扱い」(「各科目にわたる 指導計画の作成と内容の取扱い」及び「各科目にわたる内容 の取扱い」を含む。以下「学習指導要領に示す内容の取扱い」 という。)に示す事項を不足なく取り上げていること。[/color]
[color=#faa>(2) 本文,問題,説明文,注,資料,作品,挿絵,写真,図など教科用図書の内容(以下「図書の内容」という。)には,学習指導要領に示す目標,学習指導要領に示す内容及び学習指導要領に示す内容の取扱いに照らして,不必要なものは取り上げていないこと。[/color]
[color=gray>(3) 図書の内容は,生徒の心身の発達段階に適応しており,その能力からみて程度が高過ぎるところはないこと。
[/color]
とありますから。
もっとも、歴史教科書とかには、余計なことが書かれているケースが多々あるわけですが...

-
たろう
Re:プログラマの数学について
Dixq (管理人)さん回答ありがとうございます。わかりやすかったです。
これを活かししていきたいと思います。
それとプログラムでわからないことができたので。
新規投稿します。
これを活かししていきたいと思います。
それとプログラムでわからないことができたので。
新規投稿します。