力学の入門 : 3 「微分と積分(1)」

GRAM · 投稿記事 by **GRAM** » 13年前

予告通り、微分積分の話をします。　取りあえず微分の説明をしようと思います。
とはいってもこの辺話し始めると終わらないので、代表的な話を取り上げて、
他の細かい話は出て来るたびに触れる感じで行きたいと思います。

[ 1 ] 微分

微分についてのさわりの話はもうしました。
というのも、速度の一番最初の話で、
「速度とはs-tグラフの傾きである」ということに触れたと思います。

微分とはまさに関数の任意の座標の接線の傾きを求める作業に他ならないのです

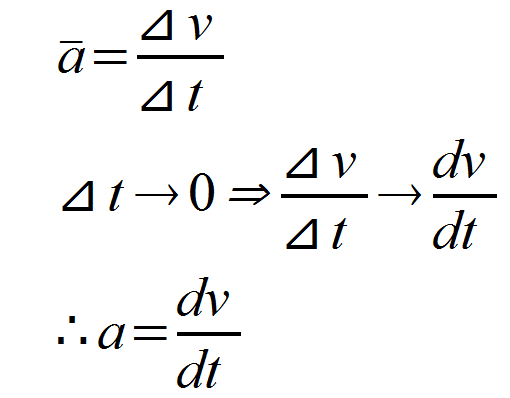
: 加速度公式.png (9.35 KiB) 閲覧数: 73 回

さて、今一番最初の公式は、前回の平均加速度を導出する公式でした。
加速度とは、「この微小な時間⊿tを0に近づけていったときの平均加速度」ということができました。
その様子を表したのが2つ目の式です。
⊿t　　　　　　　　　　　　→ 0　　　　　　　⇒　　　　　⊿v / ⊿t =　dv /dt
(時間の変化量を)　　(0に近づけた)　(ならば)　　(⊿v/⊿tはv-tグラフでその時間の接線の傾きと一緒になるよ)
・・・という意味です。

ここで、dv / dt を求めること。　すなわちv-tグラフの任意の時刻の接線の傾きを求めることを
「v　を　tで微分する」　といいます。

第3式ですが、この値は加速度aと等しくなります。これは「加速度がv-tグラフの接線の傾きだ」という事実から明らかですね。
もっとも本来「加速度aは速度vを時間tで微分したものである」というのが加速度の定義だったりします。

またdv / dt は　本来( d / dt )*vのことで、tで微分するなら、前に d/ dtを、　適当な変数xで微分するなら　d / dxを前にかければ「微分してるんだよ！」とアピールできます。

さて、微分のイメージ自体は接線の傾きを求める作業として差し支えないのですが、もちろん求める公式のようなものがあります。

今 y　が　xの関数であることを y = f(x)と書きます。（y = xならf(x) = x, y = x^2なら　f(x) = x^2）
このとき、yをxで微分してみましょう。
つまりdy / dx を求めればいいわけです。
微分することは見かけ上　d / dx　を掛けることにできて、当然等号を成り立たせるよう両辺にd / dxを掛けると

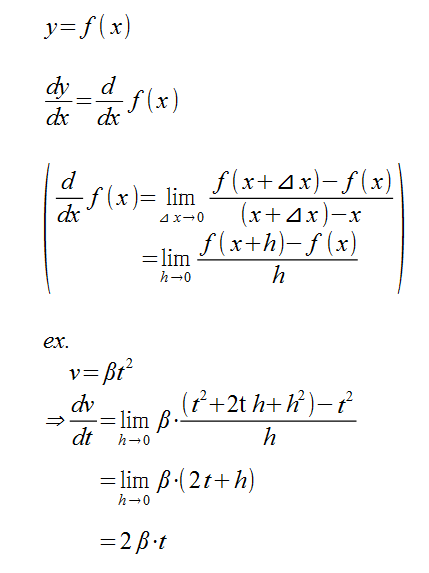
: 微分.png (24.13 KiB) 閲覧数: 58 回

はい。第１式の (d / dx )* f(x) を求める方法は次の括弧内の公式です。
難しいように見えますが、⊿xを0に近づけることをlim(⊿x⇒0)と書いているだけで、あとは特に変わっていません。

f(x)とはあるｘ座標に対応するy座標、　f(x+⊿x)とはその座標のすぐ隣のグラフ上の点のy座標で、
後は
yの増加量 / xの増加量 ・・・という中学校2年の公式で傾きを求めています。
最後は⊿xをhに書き直した式です。　⊿xのほうがわかりやすいのですが教科書によく載っているのはこっちです。

exのところでは　速度v　が　βt^2であらわされているときの、　加速度を求めています。（ベータはどんな数でもok）
一番最後にhが残っていますが、0に近づけると消えてなくなってしまうので、最終的に
dv / dt = 2βtとなります。
これはたとえばβ = 1なら、
1秒後の加速度は2 ,
2秒後の加速度は4,
5秒後の加速度は10
・・・という結果を示しています。

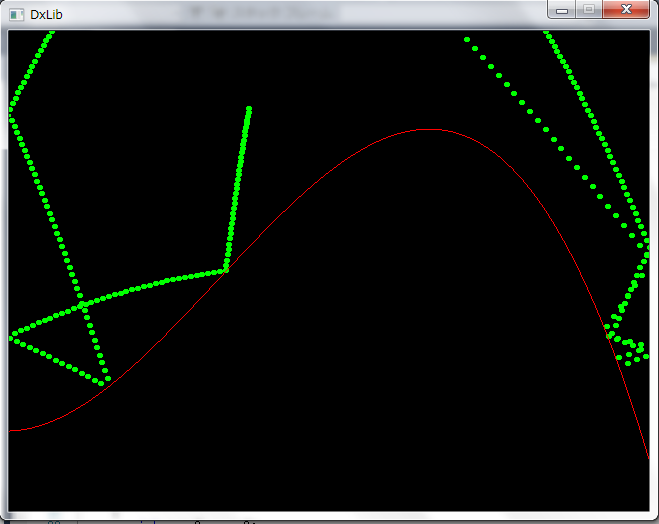
次のプログラムは　グラフ上の任意の座標の接線を求めています。
傾き( k )と座標(x0, y0)が定まっているとき、その直線の方程式は
y - y0 = k ( x - x0)
で求まります。

► スポイラーを表示

CODE:

#include 
#include 

// 3次関数を表すクラス
// f(x) = ax^3 + bx^2 + cx + d
class CubicFunction 
{
public:
	CubicFunction( double a, double b, double c, double d )
		:a_(a),b_(b),c_(c),d_(d)
	{

	}

	double GetFx( double x)
	{
		return a_*x*x*x + b_*x*x + c_*x + d_;
	}

	//dF / dx を返します。
	double GetdFdx( double x )
	{
		return a_*3*x*x + b_*2*x + c_;
	}

	void Draw()
	{
		int x = 0, y = 0;
		int oldX = 0, oldY = static_cast( GetFx(0) );
		for( x = 1; x ( GetFx(x) );
			DxLib::DrawLine( oldX, oldY, x, y, 0xFF0000 );
			oldX = x; oldY = y;
		}
	}
private:
	double a_;
	double b_;
	double c_;
	double d_;


};




int WINAPI WinMain( HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow )
{
	ChangeWindowMode(true);
	if( DxLib_Init() 
#include 
#include 
using namespace Linear;



// 3次関数を表すクラス
// f(x) = ax^3 + bx^2 + cx + d
class CubicFunction 
{
public:
	CubicFunction( double a, double b, double c, double d )
		:a_(a),b_(b),c_(c),d_(d)
	{

	}

	double GetFx( double x)
	{
		return a_*x*x*x + b_*x*x + c_*x + d_;
	}

	//dF / dx を返します。
	double GetdFdx( double x )
	{
		return a_*3*x*x + b_*2*x + c_;
	}

	void Draw()
	{
		int x = 0, y = 0;
		int oldX = 0, oldY = static_cast( GetFx(0) );
		for( x = 1; x ( GetFx(x) );
			DxLib::DrawLine( oldX, oldY, x, y, 0xFF0000 );
			oldX = x; oldY = y;
		}
	}
private:
	double a_;
	double b_;
	double c_;
	double d_;


};


namespace Constant
{
	static const double dt = 1.0 / 60.0;
}

//　ボールを表すクラス
class Ball
{
public:
	Ball( double m, Vector s, Vector v, Vector a)
		:m_(m), s_(s), v_(v), a_(a)
	{
	}

	void AddForce( Vector F )
	{
		a_ += F / m_;
	}

	void Update()
	{
		v_ += a_ * Constant::dt;
		s_ += v_ * Constant::dt;
		a_ = Vector();
	}

	void Draw()
	{
		int x = static_cast(s_.x);
		int y = static_cast(s_.y);
		DxLib::DrawCircle( x, y, 2, 0x00FF00 );
	}

	double M(){ return m_; }
	Vector S() { return s_; }
	void CorrectS( Vector s){ s_ = s; }
	Vector V() { return v_; }
	Vector A() { return a_; }


private:
	double m_;
	Vector s_;
	Vector v_;
	Vector a_;
};

class CollisionDetector
{
public:
	CollisionDetector( Ball* b, CubicFunction* f )
		:ball_(b), function_(f)
	{
	}

	void Update()
	{

		Vector S = ball_->S(); 
		double m = ball_->M();
		double dt = Constant::dt;
		ball_->AddForce( Vector( 0.0, 196*m, 0.0 ) );

		//壁面との衝突
		if( S.x  640 )
		{
			ball_->AddForce( Vector( -ball_->V().x*m*2.0*0.95 / dt, 0.0, 0.0 ) );
			ball_->CorrectS( Vector( S.xS().y, 0.0 ) );
		}
		if( S.y > 480 )
		{
			ball_->AddForce( Vector( 0.0, -ball_->V().y*m*2.0*0.95 / dt, 0.0 ) );
			ball_->CorrectS( Vector( ball_->S().x, 480.0, 0.0 ) );
		}


		Vector futureS = S + ball_->V() * dt;

		//もしも関数との交点があれば
		if( futureS.y > function_->GetFx( futureS.x ) )
		{
			//3次関数の交点を求めるのは大変なので、直線近似します。
			//時間変化が微小であれば、これは数値的に微分することになります。
			double y1 = function_->GetFx( S.x );
			double y2 = function_->GetFx( futureS.x );

			//結局衝突した部分の傾きは次のようになります
			Vector grad( futureS.x - S.x, y2 - y1, 0.0 );
			Vector rotGrad = Linear::GetNormalVector2D( grad );

			Vector dv = Linear::GetComponent( ball_->V(), rotGrad );

			ball_->AddForce( -dv*(m*2.0 / dt*0.95) );
			ball_->CorrectS( Vector( ball_->S().x, y1, 0.0 ) );
		}


	}

private:
	Ball* ball_;
	CubicFunction* function_;
};


int WINAPI WinMain( HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow )
{
	ChangeWindowMode(true);
	if( DxLib_Init() ( 450.0, 0.0, 0.0 ), Vector( 470.0, 520.0, 0.0 ), Vector() );

	CollisionDetector cd( &b, &c );


	while( ProcessMessage() == 0 && CheckHitKey( KEY_INPUT_ESCAPE ) == 0 )
	{
		//ClearDrawScreen() ;
		//メインループ
		{
			c.Draw();

			cd.Update();

			b.Update();
			b.Draw();
			


		}
		ScreenFlip() ;
	}

	DxLib_End() ;
	return 0 ;
}

: 放物線.png (45.37 KiB) 閲覧数: 65 回

次は積分です
To be Continued...

		6月 2025
日	月	火	水	木	金	土
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30