



![]()
章:レーザーを作ってみよう
作製難易度:★★★★★★★★ (8/10)
実行結果
東方に似た弾幕を作っていこうとすると製作の壁にぶつかるのがレーザーですね。
レーザーって一体どんな構造になってるんだろう?
それは皆が疑問に思うことだと思います。
ここでは、私が私なりに考えたレーザーの実装方法について紹介します。
ですので、これがゲーム業界で一般的に使われている方法かどうかは全く解りませんし、
適切な方法であるかどうかも知りませんのでその辺ご了承下さい。
また、ピタゴラスの定理、直線と点との距離やベクトルの話が出てきます。
基本的な数学のお話程度ですが、もしそんなの忘れてしまった!という人がいたら、
わからないキーワードをググりながらご覧下さい。
初めに、レーザーの基本的な考え方からご説明します。
上の図の赤い長方形部分が当たり判定です。
レーザーの画像を表示したらその特定の長方形部分を当たり判定とします。
こうすることで、小さくも、大きくも、斜めにも、真っ直ぐにもどうにでも出来ます。
画像を指定4点で描画するには
DrawModiGraph関数
を使用します。これを使う事で、どのような向きの長方形にでも出来ますね。
では、当たり判定はどうやって作ればいいでしょう。
ここで問題になるのが、「長方形と円との接触」です。
直線と点との距離や、円と円との距離を計る為の方程式は有名なものがりますが、
長方形と円との接触を判定するには一筋縄では、いきません。
以下の手順を踏んで判定を試みます
1 円の中に長方形の頂点が無いか
→あるなら接触している
→無いなら次の判定式での判定を試みる
2 長方形の中に円が入り込んでいないか
→入り込んでいるなら接触している
→無いなら次の判定式での判定を試みる
3 円の中心と辺との距離が半径以内か
→以内なら接触している
→以外なら晴れて完全に接触していないことがわかる
まずは「1 円の中に長方形の頂点が無いか」について見て行きましょう
これは、「頂点と円の中心」の距離を一つずつ見ていけばいいだけなので簡単です。
・ピタゴラスの定理を使って点と点との距離を計る
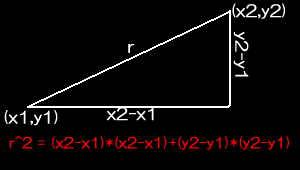
よって
r = sqrt( (x*x) + (y*y) )
です。このrが円の半径以内か以外かで、接触判定を行います。
//点が円の中にあるかどうか。0:なし 1:あり
double question_point_and_circle(pt_t p, pt_t rp,double r){
double dx=p.x-rp.x,dy=p.y-rp.y;
if(dx*dx + dy*dy < r*r) return 1;
else return 0;
}
/*中略*/
/*円の中に長方形の4点のうちどれかがあるかどうか判定*/
for(i=0;i<4;i++){
if(question_point_and_circle(pt[i],rpt,r)==1)
return 1;
}
このようにかけばそれが実装出来ますね。
次は「2 長方形の中に円が入り込んでい無いか」について見て行きましょう
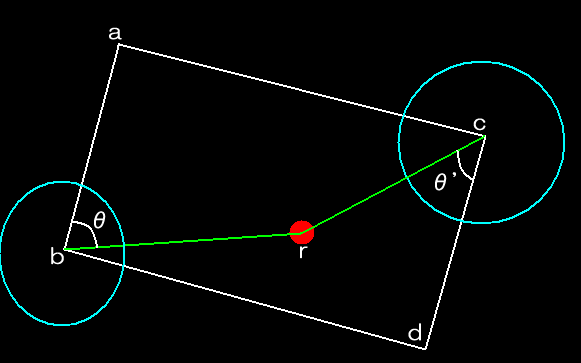
a,b,rで成す角θも、d,c,rで成す角θ'もπ/2以内であれば、長方形の中に円の中心が存在することがわかりますよね。
ではこのθを求めてみましょう。
ベクトルAとベクトルBを元にcosθを求める方法高校の時こうならいましたよね。

C言語では以下のように簡単に求められます。

これを実装してみましょう。
/* 2次元ベクトル */
typedef struct {
double x, y;
} Vector2_t;
/* diff ← ベクトル p - q */
void Vector2Diff(Vector2_t *diff, const Vector2_t *p, const Vector2_t *q)
{
diff->x = p->x - q->x;
diff->y = p->y - q->y;
}
/* ベクトル p と q の内積 */
double Vector2InnerProduct(const Vector2_t *p, const Vector2_t *q)
{
return p->x * q->x + p->y * q->y;
}
/* ベクトル p と q の外積 */
double Vector2OuterProduct(const Vector2_t *p, const Vector2_t *q)
{
return p->x * q->y - p->y * q->x;
}
/*中略*/
/* ベクトル C→P と C→Q のなす角θおよび回転方向を求める.*/
Vector2_t c, p, q; /* 入力データ */
Vector2_t cp; /* ベクトル C→P */
Vector2_t cq; /* ベクトル C→Q */
double s; /* 外積:(C→P) × (C→Q) */
double t; /* 内積:(C→P) ・ (C→Q) */
double theta,theta2;/* θ (ラジアン) */
/* c,p,q を所望の値に設定する.*/
c.x = pt[0].x; c.y = pt[0].y;
p.x = pt[1].x; p.y = pt[1].y;
q.x = x; q.y = y;
/* 回転方向および角度θを計算する.*/
Vector2Diff(&cp, &p, &c); /* cp ← p - c */
Vector2Diff(&cq, &q, &c); /* cq ← q - c */
s = Vector2OuterProduct(&cp, &cq); /* s ← cp × cq */
t = Vector2InnerProduct(&cp, &cq); /* t ← cp ・ cq */
theta = atan2(s, t);
次は「3 長方形の辺と円の中心との距離」について見て行きましょう
高校の時、点と直線の距離の求め方は習ったと思いますが、今回は点と「線分」との距離を求めてみます。
長方形の頂点をα、βとした時、円の中心rが長方形の中にあるか外にあるかをまず判定します。
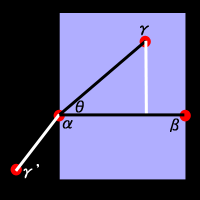
上のrように長方形の中にある場合は、ベクトルabとベクトルacが成す角θにおいて
cosθ>0となるはずです。
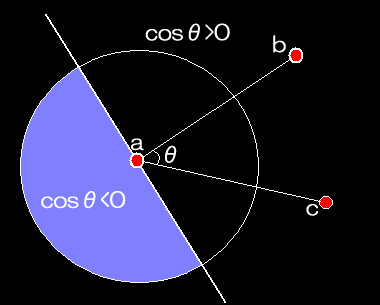
長方形の中にあるのなら、rから直線αβに垂直に線を降ろした垂線が距離となります。
これは垂線のベクトルと線分αβとの内積が0になることを用いて以下のように実装出来ます。
//点と線分との距離を求める
double get_distance(double x, double y, double x1, double y1,
double x2, double y2){
double dx,dy,a,b,t,tx,ty;
double distance;
dx = (x2 - x1); dy = (y2 - y1);
a = dx*dx + dy*dy;
b = dx * (x1 - x) + dy * (y1 - y);
t = -b / a;
if (t < 0) t = 0;
if (t > 1) t = 1;
tx = x1 + dx * t;
ty = y1 + dy * t;
distance = sqrt((x - tx)*(x - tx) + (y - ty)*(y - ty));
return distance;
}
/*中略*/
/*線分と点との距離を求める*/
for(i=0;i<4;i++){
if(get_distance(rpt.x,rpt.y,pt[i].x,pt[i].y,pt[(i+1)%4].x,pt[(i+1)%4].y)<r)
return 1;
}
これらを一つのレーザーの判定関数として実装してみましょう。
---- out_lazer.cppを新規追加し、以下を追加 ----
#include "../include/GV.h"
#include <math.h>
#include <stdio.h>
/* 2次元ベクトル */
typedef struct {
double x, y;
} Vector2_t;
/* diff ← ベクトル p - q */
void Vector2Diff(Vector2_t *diff, const Vector2_t *p, const Vector2_t *q){
diff->x = p->x - q->x;
diff->y = p->y - q->y;
}
/* ベクトル p と q の内積 */
double Vector2InnerProduct(const Vector2_t *p, const Vector2_t *q){
return p->x * q->x + p->y * q->y;
}
/* ベクトル p と q の外積 */
double Vector2OuterProduct(const Vector2_t *p, const Vector2_t *q){
return p->x * q->y - p->y * q->x;
}
//点と線分との距離を求める
double get_distance(double x, double y, double x1, double y1,
double x2, double y2){
double dx,dy,a,b,t,tx,ty;
double distance;
dx = (x2 - x1); dy = (y2 - y1);
a = dx*dx + dy*dy;
b = dx * (x1 - x) + dy * (y1 - y);
t = -b / a;
if (t < 0) t = 0;
if (t > 1) t = 1;
tx = x1 + dx * t;
ty = y1 + dy * t;
distance = sqrt((x - tx)*(x - tx) + (y - ty)*(y - ty));
return distance;
}
//点と点との距離を返す
double get_pt_and_pt(pt_t p1, pt_t p2){
return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
}
//点が円の中にあるかどうか。0:なし 1:あり
double question_point_and_circle(pt_t p, pt_t rp,double r){
double dx=p.x-rp.x,dy=p.y-rp.y;
if(dx*dx + dy*dy < r*r) return 1;
else return 0;
}
//入れ替え
void swap_double(double *n, double *m){
double t=*m;
*m=*n;*n=t;
}
//3点から角度を返す
double get_sita(pt_t pt0,pt_t pt1,pt_t rpt){
/* ベクトル C→P と C→Q のなす角θおよび回転方向を求める.*/
Vector2_t c, p, q; /* 入力データ */
Vector2_t cp; /* ベクトル C→P */
Vector2_t cq; /* ベクトル C→Q */
double s; /* 外積:(C→P) × (C→Q) */
double t; /* 内積:(C→P) ・ (C→Q) */
double theta; /* θ (ラジアン) */
/* c,p,q を所望の値に設定する.*/
c.x = pt0.x; c.y = pt0.y;
p.x = pt1.x; p.y = pt1.y;
q.x = rpt.x; q.y = rpt.y;
/* 回転方向および角度θを計算する.*/
Vector2Diff(&cp, &p, &c); /* cp ← p - c */
Vector2Diff(&cq, &q, &c); /* cq ← q - c */
s = Vector2OuterProduct(&cp, &cq); /* s ← cp × cq */
t = Vector2InnerProduct(&cp, &cq); /* t ← cp ・ cq */
theta = atan2(s, t);
return theta;
}
//長方形と円との当たりを判定する
int hitjudge_square_and_circle(pt_t pt[4], pt_t rpt, double r){
int i;
double a[4],b[4];//a:傾き b:y切片
double x=rpt.x,y=rpt.y;
/*円の中に長方形の4点のうちどれかがあるかどうか判定*/
for(i=0;i<4;i++){
if(question_point_and_circle(pt[i],rpt,r)==1)
return 1;
}
/*ここまで*/
/*長方形の中に物体が入り込んでいるかどうかを判定判定*/
theta =get_sita(pt[0],pt[1],rpt);//3点の成す角1
theta2=get_sita(pt[2],pt[3],rpt);//3点の成す角2
if(0<=theta && theta<=PI/2 && 0<=theta2 && theta2<=PI/2)
return 1;
/*ここまで*/
/*線分と点との距離を求める*/
for(i=0;i<4;i++){
if(get_distance(rpt.x,rpt.y,pt[i].x,pt[i].y,pt[(i+1)%4].x,pt[(i+1)%4].y)<r)
return 1;
}
/*ここまで*/
return 0;//どこにもヒットしなかったらぶつかっていない
}
int out_lazer(){
int i,j;
pt_t sqrp[4],rpt={ch.x,ch.y};//長方形の4点と円の中心
//レーザー分ループ
for(i=0;i<LAZER_MAX;i++){
//レーザーが登録されていて、当たり判定をする設定なら
if(lazer[i].flag>0 && lazer[i].hantei!=0){
for(j=0;j<4;j++){/レーザーの4点を設定
sqrp[j].x=lazer[i].outpt[j].x;
sqrp[j].y=lazer[i].outpt[j].y;
}
//長方形と円との接触判定
if(hitjudge_square_and_circle(sqrp,rpt,CRANGE))
return 1;
}
}
return 0;
}
また以前物理的な動きで敵を制御しましたが、レーザーも綺麗に回転して、決まった座標付近で次第にゆっくりになり
ぴたっと止まる演出をする場合がありますから、これも物理的に計算してみます。
レーザーの回転する速さをここでは角速度と言っておきます。
物理的な意味での角速度とは少し違いますのでご了承下さい。
力学の3大公式から、レーザーの回転する速さを導いて見ましょう。

Aが導けました。tyカウントかけてθmax角回転させたい時の方程式が出来上がりましたから、
この方程式に従って角度を計算すれば綺麗に加速させる事が出来ます。
また、レーザーを実装するのに以下を追加します。
---- struct.h 追加 ----
//レーザーの物理的計算を行う為の構造体
typedef struct{
int conv_flag;//回転するかどうかのフラグ
double time,base_ang,angle;//回転時間、ベースとなる角度、角度
double conv_x,conv_y,conv_base_x,conv_base_y;//回転前の座標、回転の基準となる座標
}lphy_t;
//レーザーの構造体
typedef struct{
int flag,cnt,knd,col,state;//フラグ、カウンタ、種類、色
double haba,angle,length,hantei;//幅、角度、長さ、判定範囲(表示幅に対して0~1で指定)
pt_t startpt,disppt[4],outpt[4];//レーザーを発射する始点、表示座標、当たり判定範囲
lphy_t lphy;
}lazer_t;
---- boss_shot.cpp に赤字部を追加 ----
void enter_boss(int num){
if(num==0){//中ボス開始時の時は
memset(enemy,0,sizeof(enemy_t)*ENEMY_MAX);//雑魚敵を消す
memset(shot,0,sizeof(shot_t)*SHOT_MAX);//弾幕を消す
boss.x=FMX/2;//ボスの初期座標
boss.y=-30;
boss.knd=-1;//弾幕の種類
}
boss.flag=1;
boss.hagoromo=0;//扇を広げるかどうかのフラグ
boss.endtime=99*60;//残り時間
boss.state=1;//待機中状態に
boss.cnt=0;
boss.graph_flag=0;//描画フラグを戻す
boss.knd++;
boss.wtime=0;//待機時間を初期化
memset(lazer,0,sizeof(lazer_t)*LAZER_MAX);//レーザー情報を初期化
memset(&boss_shot,0,sizeof(boss_shot_t));//ボスの弾幕情報を初期化
input_phy(60);//60カウントかけて物理的計算で定位置に戻す
}

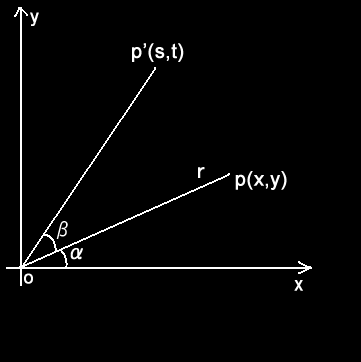
レーザーは回転します。しかも、回転基準点と離れた位置で回転します。
そこで、
どこから回転するかというconv_x,conv_y
どこを基準に回転するかというconv_base_x,conv_base_y
どこからレーザーを発射するかというstartpt.x,startpt.y
を設定し、座標の回転を使って座標変換します。
pをβ角回転して移動したp’は以下のように計算出来ます。
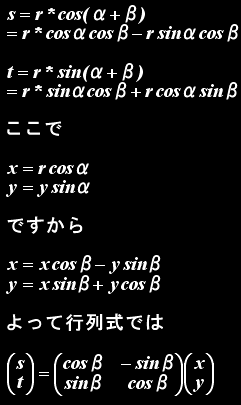
よってこの座標をコンバートする関数を
//座標回転
//(x0,y0)から(mx,my)を基準にang角回転した角度を(x,y)にいれる
void conv_pos0(double *x, double *y, double x0, double y0, double mx, double my,double ang){
double ox=x0-mx,oy=y0-my;
*x=ox*cos(ang) +oy*sin(ang);
*y=-ox*sin(ang)+oy*cos(ang);
*x+=mx;
*y+=my;
}
として実装しました。
レーザーの幅は「haba」で設定します。
レーザーの長さは「length」で設定します。
レーザーの当たり判定範囲はhanteiで設定します。0〜1の値を代入し、表示している幅のどれ位の範囲に設定するか決めます。
これらの結果を全て実行結果で見せるのは難しいので、
次の章で紹介する反魂蝶をレーザーの当たり判定ありで描画した結果を示します。
弾幕については次の章をご覧下さい。
謝辞:
この理論はC言語何でも質問サイトの回答者の皆様のご意見も参考にさせて頂きました。
ありがとうございました。
- Remical Soft -