プログラマ専用SNS ミクプラ

　はじめまして、桃印と申します。

　こちらの講座を参考にしつつシューティングゲームを製作しているのですが、
　円と矩形（四角）の当たり判定を製作する部分で行き詰ってしまいました。
　矩形が傾いていない時の判定は出来るのですが、矩形が傾いていた場合の判定計算の方法がわからないのです。

　そこで過去ログを探っていたところ、管理人様がこちら（http://www.play21.jp/board/formz.cgi?ac ... &rln=24727）で分かりやすい判定方法を提示なさっていました。
　分からないながらも自分なりに考えたところ、円から伸ばした十字（それぞれ四角の縦横に平行なもの）と四角から伸ばした十字（Ｘ軸Ｙ軸に対してθ分だけ傾いたもの）との交点二点の座標を求め、そのそれぞれ二つと四角の中心の距離を求め、その長さがともに「円の判定の長さ＋縦（または横）の判定の長さ」より小さければ当たりである、という処理を行えば良いと思いました。

　しかし実際にプログラムへと落とし込んでみたところ、問題の十字同士の交点の座標を算出する方法がわかりません。
　どなたか考え方なりヒントだけでも教えていただけないでしょうか。よろしくおねがいします。

　一応、当たり判定を考える上で使っているプログラムのソースも載せておきます。
　キーボード入力で円（当たり判定）が動きます。読み込んでいる画像は50×15ピクセルの塗りつぶしの四角です。
　環境：WindowsXP VC++ 2008EE DXライブラリ

#include "DxLib.h"
#include "math.h"
#define PI 3.1415926535898

char Key[256];
int KeyBuf;
int image;
int hit=0;

double cx=200, cy=200;
double ex_cx=0, ex_cy=0;
double c_range=10;
double ex=640/2, ey=480/2;
double tate=25, yoko=15;
double ANGLE=0*(PI/180);//傾けたい角度

double x[4],y[4];//四角形の頂点四つの座標
double kyori[4],kyori_x,kyori_y;//当たり判定と比べる距離

int WINAPI WinMain( HINSTANCE hInstance, HINSTANCE hPrevInstance,LPSTR lpCmdLine, int nCmdShow ){
	if( ChangeWindowMode(TRUE) != DX_CHANGESCREEN_OK || DxLib_Init() == -1 ) return -1; //初期化処理
        SetDrawScreen( DX_SCREEN_BACK );                        //描画先を裏画面に設定
        SetDrawBlendMode( DX_BLENDMODE_ADD , 256 ) ;//これは気にしなくていい。
        while(!ProcessMessage() && !ClearDrawScreen() && !GetHitKeyStateAll( Key ) && !Key[KEY_INPUT_ESCAPE]){
                //↑メッセージ処理        ↑画面をクリア         ↑キーボード入力状態取得       ↑ESCが押されると終了

			// キー入力取得
			KeyBuf = GetJoypadInputState( DX_INPUT_KEY_PAD1 ) ;
			// 上を押していたら上に進む
			if( KeyBuf & PAD_INPUT_UP ) cy -= 1 ;
			// 下を押していたら下に進む
			if( KeyBuf & PAD_INPUT_DOWN ) cy += 1 ;
			// 右を押していたら右に進む
			if( KeyBuf & PAD_INPUT_RIGHT ) cx += 1 ;
			// 左を押していたら左に進む
			if( KeyBuf & PAD_INPUT_LEFT ) cx -= 1 ;


			image=LoadGraph("1.png");//30×50の画像

			x[0]=(ex-yoko);//左上
			y[0]=(ey-tate);
			x[1]=(ex+yoko);//右上
			y[1]=(ey-tate);
			x[2]=(ex-yoko);//左下
			y[2]=(ey+tate);
			x[3]=(ex+yoko);//右下
			y[3]=(ey+tate);

			//円と四角の四点
			int i;
			for(i=0; i<4; i++){
				kyori=sqrt((cx-x)*(cx-x)+(cy-y)*(cy-y));
				if(kyori<=c_range)
					hit=1;
			}

			//ここから
			double point_x[2], point_y[2];
			point_x[0]=;//？？？
			point_y[0]=;//？？？
			point_x[1]=;//？？？
			point_y[1]=;//？？？
			kyori_y=sqrt((cx-point_x[0])*(cx-point_x[0])+(cy-point_y[0])*(cy-point_y[0]));
			kyori_x=sqrt((cx-point_x[1])*(cx-point_x[1])+(cy-point_y[1])*(cy-point_y[1]));
			//ここまで
			if(kyori_x=c_range+yoko && kyori_y<=c_range+tate)
				hit=1;

			DrawCircle(cx,cy,c_range,GetColor(255,255,255), TRUE);//円形当たり判定（自機）
			DrawRotaGraphF(ex,ey,1.0,ANGLE,image,true);//矩形当たり判定（敵機）

			if(hit==1){
				DrawString(  0,0,"○接触しています！！○",GetColor(255,255,0));
				hit=0;
			}
			else
				DrawString(300,0,"×接触していません。×",GetColor(255,255,0));
			ScreenFlip();
		}
		DxLib_End();
		return 0;
}

簡単に考えてみた感じですが

θ'-θを行い、θ''を出す。
（矩形の中心座標から円の中心座標の距離）×cos or sin(θ'')・・・この距離をA、Bとする
Aは円の中心から(point_x[1],point_y[1])の距離を指します。
Bは円の中心から(point_x[0],point_y[0])の距離を指します

また、矩形の中心からpoint_x[0],point_y[0]の角度は『θ＋90度』なので

矩形の中心座標（x,y）＋ A or B ×cos or sin(θ＋９０度)

で交点座標が出ると思うのですが、どうでしょう？

傾いていなければ判定できるのであれば、
傾いていない状態に座標変換して判定すれば良いのでは？

＞Libra様
　素早い回答ありがとうございます！

　なるほど、AとBの長さを算出するまでは自分でも思いついていたのですが、
　さらにそこからsin cosをかけてから矩形の座標に足すんですね。
　中学数学レベルですが、すっかり失念していました。

　早速プログラムに組み込んで、実際に判定できるのか実験してみた結果、
　確かに当たり判定を取ることが出来ました。
　――が、しかしここでまた一つの問題が。
　私のプログラム方法が悪かったのか、どうやら当たり判定を取る際に
　円の無効部分でも当たりと判定してしまうという結果が出ました。
　どうやら円と矩形ではなく、矩形同士の判定になってしまっているようです。

　以下が判定部分のプログラムになります。上のソースの//ここから　～ //ここまでの部分です。
　効率化は後回しにしているので、かなり回りくどいですが；

double point_x[2], point_y[2], ANGLE2, range2, A, B;
			range2=sqrt((cx-ex)*(cx-ex)+(cy-ey)*(cy-ey));//円の中心と矩形の中心の距離
			ANGLE2=atan2(cy-ey,cx-ex);//θ'-θ
			A=range2*cos(ANGLE2-ANGLE);
			B=range2*sin(ANGLE2-ANGLE);
			point_x[0]=ex+B*cos(ANGLE+(90*(PI/180)));
			point_y[0]=ey+B*sin(ANGLE+(90*(PI/180)));
			point_x[1]=ex+A*cos(ANGLE);
			point_y[1]=ey+A*sin(ANGLE);
			kyori_x=abs(sqrt((ex-point_x[1])*(ex-point_x[1])+(ey-point_y[1])*(ey-point_y[1])));
			kyori_y=abs(sqrt((ex-point_x[0])*(ex-point_x[0])+(point_y[0]-ey)*(point_y[0]-ey)));

　うーん、どこがおかしいんでしょう。それとも計算後の判断式

if(kyori_x<=c_range+yoko && kyori_y<=c_range+tate)

　がおかしいのでしょうか。

＞Sleepy様
　回答ありがとうございます！
　その通りです。そのために上で述べた「十字の交点部分の座標」を出したいのですけど、
　恥ずかしい話ですがその計算方法が思いつきませんで。
　こうして質問させていただいた次第です。

自分もシューティングで円と矩形の判定を考えているので、参考にさせていただきました。

矩形と円の当たり判定は図のような形になると考えてます。
図の灰色より内側が当たり判定。
今回矩形と矩形の判定になってしまったのは、図の紫の部分の当たり判定を抜いてないためだと考えられます。

自分なりの方法で：
図の紫の部分を抜くには、各頂点で図のA、Bのような座標を取り、角度A～Bを求めます。
角度AとBを出した後、大きい方と小さい方をソートしておく。A＜Bとなるように。
頂点から円の中心までの角度が角度A～Bに入っている時、頂点からの距離が円の半径より大きいの時が当たり判定の無い部分となるので、この範囲に円の半径が入っている時当たり判定から外してやればいいと思います。

また、A、Bの出し方ですが、スレ主の最初の図より、
A:矩形の中心座標(x,y)＋(矩形の縦方向の辺の長さの半分＋円の半径）×cos or sin(θ)＋矩形の半分の長さ×cos or sin(θ＋90度)
B:矩形の中心座標(x,y)＋(矩形の縦方向の辺の長さの半分＋円の半径）×cos or sin(θ+90度)＋矩形の半分の長さ×cos or sin(θ)
をやれば求められると予想してます。
またatan2関数を使う時の返り値は-π～πなので角度A～Bの範囲がatan2関数の角度の範囲より小さくなってしまったり大きくなってしまう場合は、また新たに条件式が必要になると思います。

この方法で上手くいくのであれば、2段階の計算だけで円と矩形の当たり判定が出来るので、結構短いソース量で当たり判定ができるのではないでしょうか？

　なるほど、四角側の当たり判定の有効領域を考えたらよいのですね。

　自分なりに解釈してみたところ、角部分の座標と円の中心の角度を求め、その角度-矩形の傾きで出した角度が、
　０～９０度＋θの場合（角の箇所によって範囲は変わる？）であれば上で作った当たり判定処理を実行。
　無効だった場合は角部分の座標と円の中心の距離を求め、その距離がrangeだった場合は当たり、そうでなければ当たっていない処理を返すということだと理解しました。

　しかしそのためには角の座標が分かっていないといけないのですが、
　θ分だけ傾いている場合のそれぞれの角の座標の計算方法が分かりません。
　単純にxにcosθ、yにsinθ+90をかけただけでは出ないみたいですし（傾きは矩形の中心からの数値なので）。

　初歩的な数学だとは思うのですが、どうも思いつきません。
　どなたか計算方法を教えていただけないでしょうか。

こんばんは。
いつも質問させてもらっている者ですが、
回答者側に回るのは初めてなのでおかしな点があるかもしれませんが、参考までに。

まず、桃印さんの書いたプログラムですが、計算部分はほぼ全てあっており、予想されている通り判断式が違います。
大雑把に言えば判断式だけ誤っていますので、そこだけ変えれば一応判定は取れるようになります。
それと後のレスでは修正されていますが、一番最初に書いたソースの判断式のところで、

if(kyori_x=c_range+yoko && kyori_y<=c_range+tate)

となっていたので、一応確認してみてください。
また、最初に画像は50×15ピクセルと書いてありますが、プログラムソース中では30×50の画像というコメントがありますので、もう一度画像のサイズを確認してみるのもいいかもしれません。
DXライブラリのGetGraphSize関数で画像サイズを取得すれば一番確実ではありますが。
なお、この判定が取れるようになった事が確認出来たあとは、最初に行っている四角形の４頂点との当たり判定は無くても大丈夫なはずです。というよりも４頂点の位置が傾きに対応していないため、この状態で傾けると判定の妨げになる可能性があります。


一応こんな感じです。
確認はしましたが、間違っていたらごめんなさいm(__)m

追記：
すいません、画像を見た限りでは30×50ですね。
それなら、４頂点との当たり判定部分を無くすだけで少しマシになるはずです。
もっと厳密に判定する場合は、私にはちょっと今の所分かりません^^;
・参考画像
http://www1.axfc.net/uploader/Img/link. ... _28291.png
http://www1.axfc.net/uploader/Img/link. ... _28292.png

　柏様、回答ありがとうございます！
　画像のサイズは私のミスです、申し訳ありません。正しくは30×50です。
　また、確かに４点との距離を求める部分は不要ですね。
　この点が傾きに対応できるよう、四点が傾いたときの座標の算出方法が知りたいのですが、なかなか考えつきません；
　判断式部分がおかしいとのことですが、私の書いた判断式では「矩形同士の判定」になっているものを、修正することで「円と矩形の判定」にすることができるということでしょうか？　その場合はどのような式で判断させたら良いのでしょうか。上手く円形の部分を削れるような式、全く思いつきません……；；
　これが分かれば、かなり短い式で円と矩形の判定ができるのですが……もうちょっと考えて見ます。

前回の私のレスで、追記部分を書いたせいでごちゃごちゃになってしまいましたので、まずは一旦前回のレスの内容を以下に整理します。

まず、円と矩形の当たり判定（傾きも考慮する）については桃印さんが書かれたプログラムソースから、

int i;
  for(i=0; i<4; i++){
	kyori=sqrt((cx-x)*(cx-x)+(cy-y)*(cy-y));
	if(kyori<=c_range)
		hit=1;
  }

の部分を削除するだけで円と４頂点及び４辺の当たり判定がほぼ正確に（前回の私のレスにある画像程度）とれます。
……と思います。
確認はしたのですが、
それが桃印さんの想定されている判定と合っているかどうかがちょっと自信がないので^^;
とりあえず試しにANGLEを変え、傾いていても当たり判定が取れている事を確認してみてください。
前回のレスでは画像のサイズを勘違いしていたため判断式が違うという指摘をしてしまい、
その後気づき追記を書いた、という流れですが、
追記以前の文章を削除なりしておけばよかったのですが……混乱させてしまって申し訳ないですm(__)m

ここまでが前回のレスのまとめですが、この点は恐らく理解されていると思いますが、一応ということで。。。

で、ここからが本題の「傾きにも対応した４頂点の座標」の求め方です。
とりあえず右上の点だけを考えてみることにします。
まず、この四角形はPI、つまり０°～１８０°の間で傾きます。
０°～１８０°の間で回転すると思ってもらっても大丈夫です。
四角形が回転すると、右上の座標も当然一緒に回転します。
回転するということは、その回転する為の中心座標が存在することになりますが、
この場合は四角形の中心、つまり(ex,ey)です。
右上は(ex,ey)を中心にして回転している事になります。
どこを中心にして回転しているかが分かれば、次に求めるのは、
その点（この場合は右上）は中心からどの角度でどれだけの大きさ（長さ）の位置にあるのかを求める事になります。

まずは中心と右上の角度を求めましょう。
例えば、これはatan2関数で求めればいい事が分かると思います。
次は中心からどれだけの大きさ(長さ)の位置にあるかです。
例えば、これは三平方の定理（ピタゴラスの定理）を使って求めることが出来ます。

角度、大きさが求まりましたので、これで中心から見た右上の座標が求められるはずです。
ヒントとしては、、、

x[1] = ex + cos(?) * ?;
y[1] = ey + sin(?) * ?;

という感じです。
まとめると、
１．回転の中心座標(ex,ey)と右上の角度を求める。
２．回転の中心座標(ex,ey)と右上の大きさ（長さ）を求める。
３．上記のヒントと合わせながら、求めた値をどう使えば良いか考える。
です。
ちなみに変数ANGLEも当然上記の式のどこかに入れなければいけません。

これはあくまでも一例であり、他にいくらでも簡単なやり方はあると思いますのでその点ご注意ください。
桃印さんのやりたい事と私の解釈にもしかしたらズレがあるかもしれませんが、
少しでも参考になれば幸いです。

座標変換は検索すればいくらでも出てきますよ。
http://www.google.co.jp/search?hl=ja&q= ... =&aq=f&oq=

計算は毎回行うよりも計算結果をテーブル化しておくと高速になります。
円と矩形の相対角度毎の中心間の最短距離を事前に計算しテーブル化し、
相対角度をキーにテーブルから計算済みの最短距離を求めるのです。
求めた最短距離と2点間の距離を比較し当たり判定が可能です。

テーブルでの相対角度の分解能は最小移動ドットの1/4程度で大丈夫でしょう。

＞柏様
　回答ありがとうございます。
　私のミスで混乱させてしまってすいません；
　そして本題の「傾きにも対応した４頂点の座標」ですが、
　柏様のヒントと照らし合わせて試行錯誤してみたところ、
　なんとか完成できました！

//傾きに対応している頂点四つ
			x[0]=ex-kyori[0]*cos(ANGLE+atan2(tate,yoko));//左上
			y[0]=ey-kyori[0]*sin(ANGLE+atan2(tate,yoko));
			x[1]=ex+kyori[1]*cos(-ANGLE+atan2(tate,yoko));//右上
			y[1]=ey-kyori[1]*sin(-ANGLE+atan2(tate,yoko));
			x[2]=ex-kyori[2]*cos(-ANGLE+atan2(tate,yoko));//左下
			y[2]=ey+kyori[2]*sin(-ANGLE+atan2(tate,yoko));
			x[3]=ex+kyori[3]*cos(ANGLE+atan2(tate,yoko));//右下
			y[3]=ey+kyori[3]*sin(ANGLE+atan2(tate,yoko));

　kyori[0~1]はそれぞれの点と円の中心の大きさ（長さ）です。
　これで与えた座標と円の中心の距離を求めることで、当たりの判定処理を行いました。
　ANGLEを適当なフレームごとに回転させて実験してみたところ、ばっちり当たり判定を取ることが出来ました！
　後は円の中心が無効部分でない場合の時に、上で作ったプログラムを実行させたら矩形と円形の当たり判定の完成です。

＞Sleepy様
　回答ありがとうございます。　
　すいません、もっと詳しく検索しておくべきでした……。
　テーブル化とのことですが、確かに今回完成させたプログラムの計算方法は負担の大きい、処理の重いものであることは間違いないので、Sleepy様のお言葉通り軽量化してみたいと思います。

　さて、判定処理の計算部分は完成しましたので、これで一応の解決とさせていただきます。
　Libra様、Sleepy様、柏様、ご助力ありがとうございました！

確か、線分と円の判定で、線分に幅を持たせた判定方法を取れば、
矩形と円の判定を取ることができるはずです。

ただ、これにはベクトルや内積・外積を使うので、理解が難しいかもしれませんが。

　御津凪様、回答ありがとうございます！
　そもそも今回の判定方法を使うことになったのは、
　恥ずかしい話ですが私がベクトルや内積・外積を理解できなかったからなんです。
　公式や解説を見ても、それをプログラムへと落とし込む方法がいまいち分からない。
　ただ逃げてばっかりでは勉強にならないので、いつかまたリベンジするつもりです。

円と四角形の当たり判定について、ま～くさんとＫ様にご指導いただきました。
その方法を以下に紹介します。



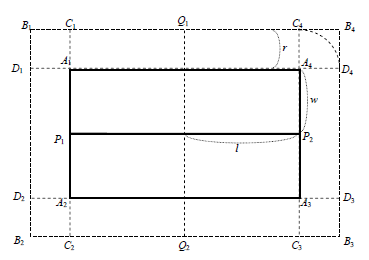
(それぞれの条件は独立したものじゃないので、あわせてご覧下さい)

これをプログラムで実装したのが

// 四角形(p1-p2, width)と円(pt, r)の当たり判定
// p1x    : 四角形中心線分の始点x
// p1y    : 四角形中心線分の始点y
// p2x    : 四角形中心線分の終点x
// p2y    : 四角形中心線分の終点y
// width  : 四角形の幅
// px     : 円の中心x
// py     : 円の中心y
// radius : 円の半径
bool
hittest (double p1x, double p1y, double p2x, double p2y,
         double width,
         double px, double py,
         double radius)
{
  double l = sqrt ((p2x - p1x) * (p2x - p1x) + (p2y - p1y) * (p2y - p1y)) / 2.0;
  double w = width / 2.0;
  double r = radius;

  double Pa = p2y - p1y;
  double Pb = p1x - p2x;
  double Pc = -Pa * p1x - Pb * p1y;

  double cx = (p1x + p2x) / 2.0;
  double cy = (p1y + p2y) / 2.0;

  double Qa = -Pb;
  double Qb = Pa;
  double Qc = Pb * cx - Pa * cy;

  double lp = fabs (Pa * px + Pb * py + Pc) / sqrt (Pa * Pa + Pb * Pb);
  double lq = fabs (Qa * px + Qb * py + Qc) / sqrt (Qa * Qa + Qb * Qb);

  return (lp <= w && lq <= l
          || (lp <= w + r && lq <= l + r
              && (lq <= l 
                  || lp <= w 
                  || (lp - w) * (lp - w) + (lq - l) * (lq - l) <= r * r)));
}

　
です。
PDFファイルをキャプチャした式を見ると若干複雑に見えるものの、
プログラムで表現するとすごく簡単に計算出来てしまうようです。
後はsqrtを使わずに計算できるように式を変更すれば高速で計算出来る関数になると思います。

ご指導下さったま～くさん、Ｋ様、本当にありがとうございますm(_ _)m

(矩形→四角形　に修正しました)

円と矩形の当たり判定なら、円の中心から矩形の一番近い場所への長さを求めて、それが円の半径より大きいかどうかを判断するだけですね。

// 点 p と 矩形 r の間の距離の平方を計算する
double SquareDistance_PointRectangle(
    double px, double py,
    double rx, double ry, double rw, double rh)
{
    double sqDist = 0.0;

    if (px < rx)      sqDist += (rx - px) * (rx - px);
    if (px > rx + rw) sqDist += (px - rx - rw) * (px - rx - rw);

    if (py < ry)      sqDist += (ry - py) * (ry - py);
    if (py > ry + rh) sqDist += (py - ry - rh) * (py - ry - rh);

    return sqDist;
}

bool TestCircleRectangle(
    double cx, double cy, double cr,
    double rx, double ry, double rw, double rh)
{
    // 円の中心と矩形 r の間の距離の平方を計算
    double sqDist = SquareDistance_PointRectangle(cx, cy, rx, ry, rw, rh);
    // 円と矩形 r が交差するのは、それらの間の平方した距離が
    // 平方した円の半径よりも小さい場合
    return sqDist <= cr * cr;
}

↑は「ゲームプログラミングのためのリアルタイム衝突判定」にあるソースを少し書き換えただけです。
こんな感じで書けば動作するのではないでしょうか。

　管理人様、名無し様、回答ありがとうございます！
　どちらのソースでも「円と矩形の判定処理」の正常動作を確認しました。
　どちらもスマートなプログラムで感動しました！
　傾いた場合に対応させる方法は、自分なりに考えてみようと思います。
　ありがとうございました～。

桃印さん

管理人さんが貼り付けたものは傾きに対応していますよ＾＾
線分（レーザーの始点と終点）の座標が変わることにより、傾いた四角形となります。
タイトルでは「矩形」とあり、矩形とは傾きなし（上、左、下、右辺）を意味する四角形
の場合が多い？ので、正確には、「円と四角形の当たり判定」というべきでしょうね＾＾；

う、、そうですね、ごめんなさい。矩形→四角形に修正しました；

　ま～く様、回答ありがとうございます！
　すいません、確かに管理人様のソースは傾きにも対応してますね……理解したつもりで全然理解できてなかったみたいです；
　また、矩形と四角形を誤解していたようでご迷惑をおかけしました。勉強が足りません；

　一応管理人様のプログラムに

start_x=ex-yoko*cos(ANGLE);
start_y=ey-yoko*sin(ANGLE);
end_x=ex+yoko*cos(ANGLE);
end_y=ey+yoko*sin(ANGLE);

if(hittest(start_x, start_y, end_x, end_y, tate*2, cx, cy, c_range)==true)
    hit=1;

　こんな感じで当たり判定処理を渡してみました。
　結果、数フレームごとに角度を変化させて実験してみても、ばっちり四角形と矩形の判定が取れました！
　かなり分かりやすく、比較的少量でかつ簡単な判定方法で素晴らしいです。
　独りで悩んでいるままでは絶対に分かりませんでした。皆様に相談して良かったです！
　今度こそ、ありがとうございました～。

矩形＝長方形 なのでそのままでいいと思いますよ。『座標に対して角度の付いてる矩形の当たり判定』とか。
四角形だと台形とかも含んでしまうので。

以前、本屋にあるシューティングゲーム作成の本を３～４冊程立ち読みしたのですが、当たり判定は円と円の判定しか記載されておらず、レーザーの当たり判定等も記載されてなかったです。
レーザーに関しては円の集合で作成し、当たり判定は円と円で行ってました。
さらに、言語がC++であったので、(Cのみの自分にとっては)本はほとんど参考にならなかったです。
自分も大変参考になりました、ありがとうございます。