プログラマ専用SNS ミクプラ

こんにちは。早速ですがテンプレートを使用して質問させて頂きます。

[1] 質問文
　[1.1] 自分が今行いたい事は何か
３４章の「長方形の中に円が入り込んでいないか」について、どうしてこうなるのか？　という疑問を解決したいと思っています。
　[1.2] どのように取り組んだか(プログラムコードがある場合記載)
龍神録プログラミングの館３４章と睨めっこしつつ、ベクトル、atan2、などの理解が不足している所は参考書なりグーグルで検索するなりして調べたという感じです。
[1.4] 今何がわからないのか、知りたいのか正直分からない事だらけで、かなり整理出来ていないのですが……とりあえずまず一番に理解したい事は、
そもそも内積と外積とは一体なんなのか？
ということです。
参考書には「内積はかけ算」と書いてありますが、ベクトルのかけ算をして出るその"内積"というものは一体どういうもので、どのような情報なのか、色々調べてはみましたがよく分かりませんでした。。。

[2] 環境 　
　[2.1] OS ： WindowsXP
　[2.2] コンパイラ名 ： VC++ 2005
[3] その他
　・使用ライブラリ
DXライブラリ。
　・どの程度Ｃ言語を理解しているか
構造体、ポインタ、ファイル入出力などなど、基本的な所は大丈夫だと思います。

非常に掴み所のない質問で申し訳ないのですが、何かアドバイスあればよろしくお願いします。
もう少し自分の中で整理出来れば質問内容を修正したいと思います。

/*追記*/
投稿してすぐに、そういえばこの章は掲示板で関係するスレッドがあった事を思い出しましたので、読んでみます。
以下、適当に理解していること、おそらくこういうことでは？と思っていることなど。
・とりあえず回転方向を考えず、角度（0°～180°）を求めるだけなら内積の定義からcosθを求め、アークコサインを使えばいいらしい。
・長方形が傾いていない事を想定するなら、内積・外積は求めずベクトルC→P,C→Qのなす角をatan2で求めれば恐らく判定出来る。

ちょっと的外れな回答になるかもしれませんが、仕様を変えてみるというのはどうでしょう？
一般的に初歩的なブロック崩しはそこまで考えられて無いと思います。

円は正方形として当たり判定を考えた方がわかりやすくないでしょうか？



この赤の部分に当たる機会はほとんどないですよね。
ブロックの角に赤の部分がもしあたったとして、それを忠実に計算して進行方向を変えるのは結構めんどくさいんじゃ無いかと思います。
正方形と長方形の当たり判定は簡単に計算できると思うので、そちらで実装してみてはどうでしょう？

もし実装してみて、これではやはり違和感があるという場合は、改めて実装してみては。

管理人さん、アドバイスありがとうございます。

まず最初に、色々と情報が少なく、質問内容が分かりづらくなってしまい申し訳ありません。。。

管理人さんが紹介してくださった短形同士の当たり判定（という表現でいいでしょうか？）ですが、難しい数学などは苦手なため、わりと楽に実装できる点と、過去に旧シューティングゲームの館のソースをいじっている時に試した事があるという点で、一度すでに実装してはいました。
おっしゃる通りブロック崩しを作成する場合、この当たり判定で全く問題ありません。
そもそもブロック崩しで、長方形に円が入り込むという状況は想定しなくても問題ないですね。。。

というわけでブロック崩しを作るうえでは問題ないのですが、将来的に色々と応用出来るかと思い、ブロック崩しを別にして「長方形と円の当たり判定」を学んでおこうと思った次第です。
……という内容を書けばよかったですねorz

とりあえず回転（傾き？）を考えない場合の「長方形の中に円が入り込んでいないか」という当たり判定は実際に動かして確認出来ましたので、もうちょっとベクトル、内積・外積について調べてみます。

・報告
３４章の、
ベクトルＡとＢの内積及び外積の定義
の所に書かれている外積の定義ですが、もしかして
Ａ×Ｂ＝Ａｘ＊Ｂｙ[color=red> - [/color]Ａｙ＊Ｂｘ
でしょうか？
一応ご報告しておきます。

あら、、x,yってどちらのx,yかわからないし、おかしな書き方が盛りだくさん・・。
書き直したいのですが、現在このPCにワードが入ってないので、明日書き直します。
後、この計算方法はもっと簡単に出来るので、そちらも合わせて作り直したいと思います。
ベクトルの内積については
http://www.geisya.or.jp/~mwm48961/kou2/ ... duct0.html
この辺とかどうでしょう？
後は高校の教科書の数学Bとかに書いてあると思うので、そちらお読みになってはいかがでしょう？

とりあえず内積・外積についての理解を深め、
少し違う方法でなんとか「（傾いた）長方形の中に円が入り込んでいないか」の判定について出来るようになりました。

ですが、３４章でご紹介されているやり方の最後、atan2に内積・外積の値を渡すと何故角度が求まるのか？　ということが理解出来ません。
一応作れた判定では、自分の理解している範囲で判定処理をしてみようということで、
内積・外積を求める所まではほぼ一緒の処理をし、
「内積は2つのベクトルの角度が90度以下のときは正、90度より大きいときは負の値になる」
と書かれたサイトがありましたので、これと回転方向（向き？）の値である外積を併用し、

内積１>0 && 内積２>0 && 外積１<0 && 外積２<0

という条件で判定処理を行いました。
が、これが分かった所でやはりatan2を使用して何故角度が求まるのかが謎です。
私の調べた限りでは、

・内積
それぞれのベクトルがどれほど近いかという値。
ＢがＡに対してどれだけがんばったかを表す値。
９０度以下か大きいかで正負の値となる。
・外積
向き、回転方向などを表す。

とのことですので、atan2にベクトルがどれほど近いか、またその向きはどちらか、
という情報を与えて角度が返ってくることが理解できない、ということです。
だいぶベクトル及び内積・外積については理解できましたが、これだけがどうにも分かりません……。

もうちょっと解り易い判定方法について、以下のような判定方法が考えられます。
図のように長方形の中心を通る辺に平行な２つの直線を考えます。



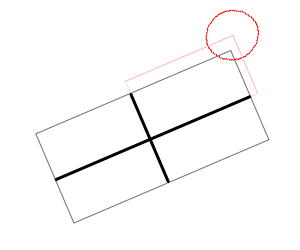
円をまずは中心点のみの点だと思います。
点から直線に垂線を下ろします。「下ろした垂線の足が線分の中で、かつ線分と点との距離が長方形の長さの半分+円の半径以内」なら接触している事がわかります。
図は直線に下ろした垂線の足が線分外なのでこの判定式にひっかかりません。
引っかからなかった場合は、長方形の頂点が円の半径の中に無いか調べます。
それでも判定式にひっかからなかったら接触していない事になります。

こっちの判定式の方がずっと簡単ですよね。点と線分の関係についてはま～くさんにアドバイス頂きました。

これを見て思ったんですが、長方形を回転させても似たようなことが出来ると思います。
長方形の横の直線の部分がx軸と重なるように回転させて下の図のようにします。



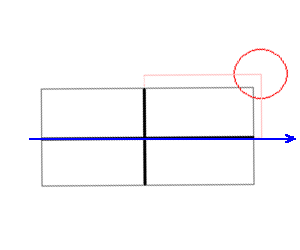
円の中心が長方形のxの範囲内ならy座標で距離を求め、円の中心が長方形のyの範囲内ならx座標で距離を求めることで、
先ほど垂線を下ろして判定したような事が出来ます。
こちらも同様に判定した後、頂点と円の中心との距離を測り、それでも判定式にあてはまらなかったら
接触していない事がわかります。

もっとよい方法があるかもしれませんので、もう少しだけ考えてみようと思います。

色々と考えましたがatan2と内積・外積の関係についてはすっきり理解できず、
それでもとりあえず最後の判定処理である「長方形の辺と円の中心との距離」についても、
ちょっと私の学力では理解出来ませんでしたが、適当に他の判定方法を考え実装することで落ち着きました。

ただその判定方法は効率が悪いため、引き続き数学に関して理解を深め、
３４章の内容が理解出来るようになりたいと思います。
あと、ご紹介して頂いた判定方法も試してみます。

アドバイスありがとうございました！