プログラマ専用SNS ミクプラ

はじめまして。

初の投稿になりますが、よろしくお願いします。



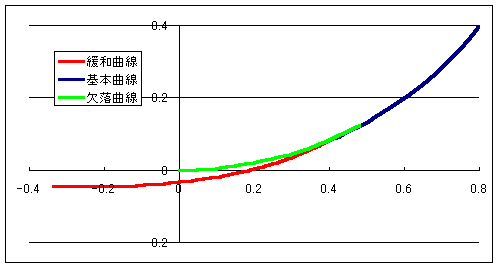
こんな感じの曲線と玉の衝突判定を組むのにはどのような物理演算を組めばよいでしょうか…？！

イメージとしてはパチンコ台の衝突判定をイメージしてもらえれば大丈夫です。

現状としては
玉と玉、玉と直線、まではなんとか理解できています。

どうぞよろしくお願いしますorz

とりあえず簡単に実装するには、曲線を適当な長さの直線(線分)に近似的に分割し、当たり判定をするという方法があります。

どの程度の精度が必要ですか？
この曲線は方程式で表せるものですか？

曲線と衝突判定する対象が玉（円かな）だけ　なのであれば
真面目にやるなら　曲線の方程式 f(x,y)=0 に対して，
|f(x,y)| や f(x,y)^2 を曲線からの距離関数として使って判定すればいいのかな．

もし，図のような曲線を適当に近似して判定してもよいということなら
折れ線の他に，複数の円弧　で近似するというのも良いかもしれませんね．

こちらの記事にあるコードは参考にならないでしょうか。
壁に沿って転がる玉:ISLeのビデオゲーム工房
複雑な図形にも対応できます。

ちなみに元ネタは↓です。

ぜぶらー さんが書きました:イメージとしてはパチンコ台の衝突判定をイメージしてもらえれば大丈夫です。

記事のコードが手抜きなのは基礎研究の最初期のシンプルなソースから拾ってるからです。
元ネタの方はここに材質のパラメータを追加し調整を加え最終的には3Dになりました。

法線を持った点群ですか…

生成が楽そうだし，当たり判定も難しいこと考えなくていいし，判定計算は軽いし
いいですね．

点の配置が疎すぎると　２つの点の間に玉がはまる　みたいなことが起きそうなので
滑らかに転がる　みたいなのをやるためにはそれなりに密な点群が必要そうですが…
玉の位置に合わせて動的に補間とかすればその点も問題ないのかな．