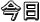
public class DiagramCalcr {

        // centerを中心に角度ang、頂点群ptを回転する
        public static void RotateDiagram(PointF pt[], final PointF center, final float ang) {
                for (int i = 0; i < pt.length; i++) {
                        RotatePt(pt[i], center, ang);
                }
        }

        // rotaPtを中心に角度ang、origPtを回転する
        public static void RotatePt(PointF rotaPt, final PointF origPt, final float ang) {
                float cx = origPt.x;
                float cy = origPt.y;
                float x = rotaPt.x;
                float y = rotaPt.y;
                rotaPt.x = (float) (cx + Math.cos(ang) * (x - cx) - Math.sin(ang) * (y - cy));
                rotaPt.y = (float) (cy + Math.sin(ang) * (x - cx) + Math.cos(ang) * (y - cy));
        }

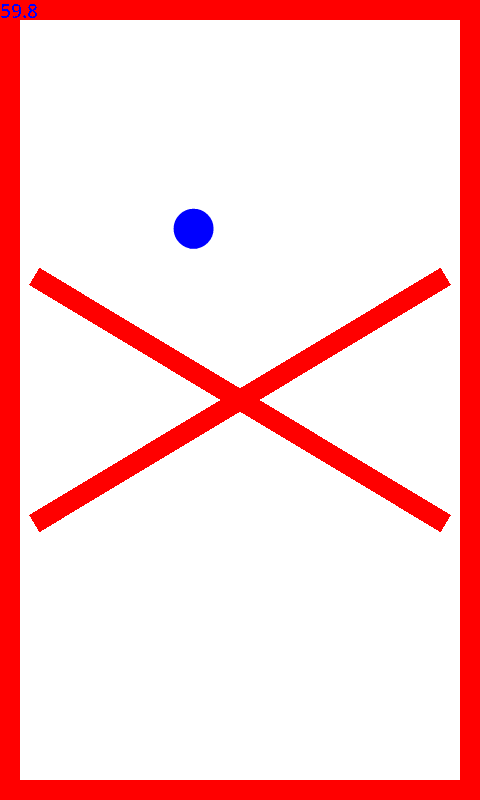
        // 頂点群ptの線分とcirが接触していたらその接触しているベクトルをverに格納してtrueを返す
        public static boolean isHit(PointF pt[], final Circle cir, Vec vec) {
                if (pt.length < 2) { // 線でなければ
                        return false;
                }
                int len = pt.length;
                for (int i = 1; i <= len; i++) {//例えば線分0-1,1-2,2-3,3-0とループさせてつなげる為%を使用してループ
                        Line line = new Line(pt[i - 1].x, pt[i - 1].y, pt[i % len].x, pt[i % len].y);
                        if (isHitLC(line, cir) == true) {//接触していれば
                                vec._x= pt[i % len].x - pt[i - 1].x;//その線分のベクトルを格納する
                                vec._y= pt[i % len].y - pt[i - 1].y;
                                return true;
                        }
                }
                return false;
        }

        //線分lineと円cirが当たっていればtrueを返す
        public static boolean isHitLC(Line L,Circle C){
                // 円と線分の当たり判定関数
                if((L._sx*(C._x-L._x) + L._sy*(C._y-L._y)) <= 0){
                        // 始点を通る､線分に垂直な線を置いたとき､円の中心が線分の範囲外にあったとき
                        // ｢線分の始点から円の中心までの距離の２乗｣と｢円の半径の２乗｣との比較
                        return (C._r*C._r >= (C._x-L._x)*(C._x-L._x)+(C._y-L._y)*(C._y-L._y));
                } else if(((-L._sx)*(C._x-(L._x+L._sx)) + (-L._sy)*(C._y-(L._y+L._sy))) <= 0){
                        // 終点を通る､線分に垂直な線を置いたとき､円の中心が線分の範囲外にあったとき
                        // ｢線分の終点から円の中心までの距離の２乗｣と｢円の半径の２乗｣との比較
                        return (C._r*C._r >= (C._x-(L._x+L._sx))*(C._x-(L._x+L._sx))+(C._y-(L._y+L._sy))*(C._y-(L._y+L._sy)));
                } else {
                        // 線分の始点終点に垂線を引っ張ったとき､円の中心がその範囲内にあったとき
                        float e = (float) Math.sqrt(L._sx*L._sx + L._sy*L._sy);   // これでx,y成分を割れば単ベクトルになる
                        float c2 = (C._x-L._x)*(C._x-L._x)+(C._y-L._y)*(C._y-L._y);
                        float b = (C._x-L._x)*(L._sx/e)+(C._y-L._y)*(L._sy/e);   // 内積で算出した､隣辺の長さ
                        return (C._r*C._r >= c2 - b*b);
                }
        }
}